Introdução

Você é proprietário de uma empresa ou profissional de TI? Nesse caso, você provavelmente está sempre em busca de maneiras de aprimorar seu produto, serviço ou algoritmo. Mudanças podem ser arriscadas, especialmente em ambientes produtivos. É difícil prever se eles beneficiarão sua empresa. É aqui que os testes A/B se tornam valiosos. O teste A/B é uma ferramenta poderosa. Ele permite que você teste diferentes versões do seu produto, serviço ou algoritmo. Isso ajuda a identificar se uma mudança terá um impacto positivo. O teste A/B usa a teoria da probabilidade para apoiar a tomada de decisão baseada em dados. Isso pode levar a um melhor engajamento, maiores taxas de conversão e aumento da receita. Neste blog, exploraremos os fundamentos do teste A/B, abordando conceitos e métodos estatísticos importantes. Começaremos discutindo a importância de selecionar o tamanho apropriado da amostra. Nós usaremos o modelo de estatísticas biblioteca para calcular o tamanho da amostra para proporções e médias. Em seguida, vamos nos aprofundar na realização de um teste z para proporções e médias e explorar como usar o bootstrapping para testes A/B. Finalmente, analisaremos alguns resultados possíveis do teste A/B e como interpretar os resultados.

Teste de latência no Google

Em 2009, o Google fez um teste A/B para estudar como a latência do site afeta o comportamento do usuário. Para esse teste, o Google dividiu o tráfego de usuários aleatoriamente em dois grupos. Um grupo visualizou páginas que foram carregadas em velocidade normal. O outro grupo visualizou páginas com um atraso deliberado de 100 a 400 milissegundos. Os resultados do teste foram surpreendentes. Mesmo um pequeno atraso de apenas 100 milissegundos levou a uma diminuição mensurável no engajamento do usuário. O grupo que teve as páginas atrasadas teve um desempenho 0,2% a 0,6% pior em várias métricas de engajamento do usuário. Isso incluiu consultas de pesquisa e cliques em anúncios. Essas descobertas fizeram com que o Google percebesse que a latência do site afeta significativamente o engajamento do usuário. Mesmo pequenas melhorias na velocidade da página podem melhorar consideravelmente o comportamento do usuário. O setor de tecnologia agora aceita amplamente essa visão. Muitas empresas agora investem pesadamente na otimização do desempenho de seus sites e aplicativos. Isso melhora o engajamento e a retenção do usuário.

Um exemplo prático do processo

Vamos considerar um exemplo prático. Suponha que você tenha um produto digital, como um site. Você quer testar se um novo design para sua página de destino melhorará as conversões ou as taxas de cliques. As variáveis que você considera dependerão do seu aplicativo comercial específico. Dois tipos comumente identificados são binários ou contínuos. As variáveis binárias podem representar se um usuário instalou um aplicativo ou não. Eles são usados para calcular as taxas de conversão (proporções). As variáveis contínuas podem ser associadas a uma média, como um custo por clique. Neste exemplo, testaremos se a nova página de destino melhora as taxas de cliques (CTR). No entanto, consideraremos os dois casos no restante do blog.

Executando um teste A/B

Para executar um teste A/B, primeiro você precisa definir dois grupos: tratamento e controle. Em seguida, você atribui indivíduos a cada grupo aleatoriamente. O tamanho de cada grupo não é trivial e discutiremos isso mais tarde. O grupo de tratamento obtém a variante para ser testada, enquanto o outro grupo permanece o mesmo. Enquanto o experimento está em execução, é crucial monitorar não apenas a métrica primária que você deseja otimizar, como a CTR. Você também deve ficar de olho em outras métricas relevantes que devem permanecer consistentes. Isso garante que quaisquer alterações feitas para melhorar a métrica primária não afetem negativamente outras métricas importantes. Depois de coletar suas amostras, você precisa analisar os resultados do teste A/B. Observando os resultados, vemos que o grupo de tratamento teve uma pontuação 1% maior do que o grupo controle. Inicialmente, isso pode parecer um resultado positivo. No entanto, é crucial garantir que esse resultado seja estatisticamente significativo. A significância estatística ajuda a quantificar se um resultado provavelmente se deve ao acaso ou a um fator de interesse.. Ao analisar os resultados de um experimento a partir de uma amostra, é possível que um grupo pareça superar o outro devido ao acaso. Mas isso pode não ser o caso. Para evitar conclusões falsas comparando dois valores absolutos, realizamos um teste de hipótese. Isso nos permite concluir com alguma confiança que os resultados obtidos não se devem apenas ao acaso.

Por que testar hipóteses

“O teste de hipóteses fornece uma estrutura objetiva para tomar decisões usando métodos probabilísticos, em vez de confiar em impressões subjetivas. As pessoas podem formar opiniões diferentes analisando os dados, mas um teste de hipóteses fornece um critério uniforme de tomada de decisão que é consistente para todas as pessoas.” - Rosner, B. Fundamentos da bioestatística.

Em testes A/B, testaremos se há uma mudança significativa em nossa métrica após implementar a variante e também a magnitude do efeito. Normalmente, formularemos hipóteses dos seguintes tipos:

• Hipótese nula (H0): A métrica é a mesma para os dois grupos. Ou seja, mean_treatment = mean_control.
• Hipótese alternativa (H1): A métrica é diferente. Ou seja, tratamento médio! = controle_médio

O processo

O procedimento padrão para o teste de hipóteses é definir as hipóteses nula e alternativa. Em seguida, determinamos se apoiamos ou rejeitamos a hipótese nula. Para fazer isso, calculamos uma estatística de teste. Isso mede a distância entre a estimativa da amostra e o valor hipotético sob a hipótese nula. Nesse contexto, ele mede a que distância a diferença computada entre os dois grupos está de zero. Isso ocorre porque a hipótese nula é que a métrica é a mesma para os dois grupos. Em seguida, usamos a estatística de teste para calcular o valor p. Isso representa a probabilidade de observar o resultado se a hipótese nula for verdadeira. Em outras palavras, representa a probabilidade de obter uma diferença como a observada. Isso pressupõe que a métrica seja a mesma para os dois grupos. Se o valor p for menor que um certo nível de significância (também conhecido como alfa), rejeitamos a hipótese nula em favor da hipótese alternativa. Quanto menor o valor de p, menor a probabilidade de os resultados serem devidos apenas ao acaso. No entanto, se o valor de p for maior ou igual ao nível de significância, não rejeitamos a hipótese nula. Isso indica que não há evidências suficientes para concluir que os grupos ou variáveis são diferentes.

Resultados possíveis

Todos os resultados em uma situação de teste de hipóteses geralmente se referem à hipótese nula. Assim, se decidirmos que H0 é verdadeiro, dizemos que aceitamos H0. Se decidirmos que H1 é verdadeiro, dizemos que H0 não é verdadeiro ou, equivalentemente, que rejeitamos H0. Portanto, há quatro resultados possíveis:

- Rosner, B. Fundamentos da Bioestatística (7ª ed.), p. 204

Idealmente, queremos aceitar H0 sempre que for realmente verdadeiro e rejeitá-lo de outra forma. Nesse contexto de tomada de decisão sob incerteza, podemos cometer dois tipos de erros. Isso porque estamos trabalhando com uma amostra e queremos testar se esses resultados podem ser extrapolados para a população.

Tipos de erros

• Erro do tipo 1: Rejeitando H0 quando é verdadeiro. Alfa (α) representa a probabilidade de cometer um erro do tipo 1, também conhecido como falso positivo. Mencionamos isso anteriormente ao definir o limite no qual rejeitamos ou não a hipótese nula.
• Erro do tipo 2: Aceitando H0 quando é falso. Beta (β) representa a probabilidade de cometer um erro do tipo 2, também chamado de falso negativo.

O resultado que mais nos interessa nesse contexto é a escolha de H1 quando ela é realmente verdadeira. A probabilidade associada é chamada de poder estatístico e é indicada por 1 − β. O poder de um teste de hipótese é a probabilidade de o teste rejeitar corretamente a hipótese nula.. É uma medida da probabilidade de, dado um determinado tamanho de amostra, detectar uma diferença estatisticamente significativa quando a hipótese alternativa é verdadeira. A baixa potência indica uma baixa probabilidade de detectar uma diferença significativa, mesmo que haja diferenças reais entre os grupos controle e experimental.

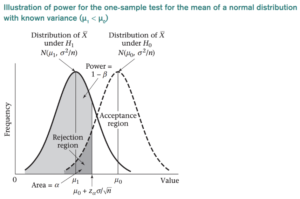
- Rosner, B. Fundamentos da Bioestatística (7ª ed.), p. 222.

Quando projetamos um experimento, geralmente definimos valores para alfa, beta (e potência). Mas também precisamos definir qual mudança esperamos ver entre os dois grupos. Que mudança importará nesse caso específico? Isso é chamado de significado prático ou também conhecido como tamanho de efeito desejado. Esses três fatores: alfa, potência e tamanho do efeito estão diretamente relacionados ao tamanho da amostra. A relação entre eles é complexa e interdependente. É um conceito muito importante de entender.

Tamanho da amostra e sua importância

O tamanho da amostra desempenha um papel fundamental no teste de hipóteses. Isso afeta os valores de alfa, beta e potência. Aumentar o tamanho da amostra geralmente diminui tanto o alfa quanto o beta, enquanto aumenta o poder. Isso ocorre porque um tamanho de amostra maior fornece mais dados e reduz o erro de amostragem. Isso facilita a detecção de um efeito verdadeiro, caso exista. Como resultado, um tamanho de amostra maior geralmente leva a uma estimativa mais precisa dos parâmetros da população. Isso, por sua vez, aumenta a potência do teste. Por outro lado, diminuir o tamanho da amostra geralmente aumenta tanto o alfa quanto o beta, enquanto diminui o poder. Isso ocorre porque, com um tamanho de amostra menor, há uma chance maior de variação aleatória afetar os resultados. Isso pode levar a uma conclusão falsa positiva ou falsa negativa. Como resultado, um tamanho menor da amostra pode diminuir a precisão da estimativa. Isso, por sua vez, diminui a potência do teste. O tamanho do efeito afeta diretamente o tamanho da amostra. Um tamanho de efeito maior geralmente requer um tamanho menor de amostra para atingir o mesmo nível de potência. Por outro lado, um tamanho de efeito menor exigirá um tamanho de amostra maior para atingir o mesmo nível de potência. O tamanho do efeito pode ser considerado como a magnitude da diferença entre os grupos que estão sendo comparados. Normalmente, é medido usando medidas padronizadas de tamanho de efeito, como o d de Cohen.

Alfa, potência e tamanho do efeito em testes A/B

Gráfico de alfa, beta e potência no caso de um tamanho de amostra pequeno versus tamanho de amostra grande para um mesmo tamanho de efeito de 0,02:

Observe que se aumentarmos o tamanho do efeito, por exemplo, de 0,02 para 0,1, o centro das distribuições ficaria mais distante, já que a distância entre 0 (o caso da hipótese nula em que os grupos têm a mesma métrica) e 0,1 é muito maior do que entre 0 e 0,02, teríamos menos erros e precisaríamos de menos dados. Isso significa que um tamanho de efeito maior pode levar a resultados mais estatisticamente significativos com um tamanho de amostra menor. Também é importante considerar o significado prático do tamanho do efeito, pois um tamanho de efeito muito pequeno pode não ser significativo, mesmo que seja estatisticamente significativo. O tamanho do efeito indica qual diferença é relevante em termos comerciais e quantifica qual mudança é importante que ocorra.. Depende do experimento que está sendo conduzido. Não é o mesmo em um contexto médico, por exemplo, em que estamos testando se um novo medicamento melhorará os resultados dos pacientes, e ao avaliar se a alteração de um recurso em um site melhorará as conversões. No primeiro caso, uma diferença de 5 a 10% pode ser considerada praticamente significativa, pois se a mudança for muito pequena, não vale a pena o custo da introdução de um novo medicamento. Por outro lado, no último caso, uma diferença de 1 a 2% pode ser relevante quando estamos falando de milhares de usuários, fazendo com que valha a pena implementar a mudança. No geral, a relação entre o tamanho do efeito e o tamanho da amostra destaca a importância de considerar cuidadosamente a questão da pesquisa e a magnitude do efeito que está sendo estudado ao projetar experimentos.

Como escolher o tamanho da amostra no teste A/B?

Determinar o tamanho da amostra é uma das etapas mais importantes na criação de um teste A/B. Um tamanho de amostra muito pequeno pode levar a resultados inconclusivos, enquanto um tamanho de amostra muito grande pode desperdiçar recursos. Portanto, é importante escolher um tamanho de amostra apropriado para seu teste A/B. Conforme mencionado anteriormente, o tamanho da amostra necessário para um teste de hipótese depende de vários fatores, incluindo o tamanho do efeito que se espera que seja observado, o nível de significância desejado, o poder do teste, o tipo de teste estatístico usado e a variabilidade dos dados. Primeiro, vamos importar a biblioteca import statsmodels.stats.api como sms Nível de significância: Isso é o que chamávamos anteriormente de alfa, um nível de significância normalmente é definido em um valor predeterminado (como 0,05 ou 0,01) e é usado em testes de hipóteses para determinar se devemos rejeitar ou deixar de rejeitar a hipótese nula. alpha = 0,05 Significado prático: Também conhecido como tamanho do efeito, se nossa variável for uma proporção e quisermos para observar se nossa CTR vai de 0,10 a 0,15, usaremos a função proportion_effectsize para obter o valor correspondente. effect_size = sms.proportion_effectsize (0,10, 0,15) Se nossa variável for uma média e quisermos ver se ela muda em 5%, também devemos levar em consideração o desvio padrão da distribuição a partir da qual estamos estimando, esse desvio pode ser calculado com base em uma amostra da população em estudo. std= 0,53 effect_size = 0,05/std Potência: Um valor de 0,8 é comumente definido como o limite de potência. potência = 0,8 Finalmente, calculamos o tamanho amostral necessário como: required_n = sms.normalindpower () .solve_power (effect_size, power=power, alpha=alpha)

Fatores que afetam o tamanho da amostra

1. À medida que o desvio padrão aumenta, o tamanho amostral necessário também aumenta.
2. Diminuir o nível de significância (diminuir α) levará a um aumento no tamanho da amostra.
3. Se a potência necessária (1 − β) aumentar, isso também levará a um aumento no tamanho da amostra.
4. O aumento da distância absoluta entre as médias nula e alternativa (|µ0 − µ1| -> tamanho do efeito) causa uma diminuição no tamanho da amostra.

O sucesso de um teste A/B depende da qualidade do projeto do experimento, da precisão dos dados coletados e do rigor da análise estatística. Portanto, certifique-se de planejar e executar cuidadosamente cada etapa do teste para obter resultados significativos que possam informar sua tomada de decisão.

Teste de hipótese

Depois de coletarmos todas as amostras que definimos como necessárias para realizar o teste, prosseguiremos com a execução. Para isso, existem diferentes opções: O teste de hipóteses pode ser realizado usando ambos métodos paramétricos, que assumem uma distribuição subjacente, como teste z e teste t, ou métodos não paramétricos, que não fazem nenhuma suposição sobre as distribuições, como o teste exato de Fisher, o teste qui-quadrado ou o teste Wilcoxon Rank Sum/Mann Whitney. Observe que a escolha entre métodos paramétricos ou não paramétricos depende dos dados que estão sendo analisados e das suposições que podemos fazer sobre a população subjacente. Por exemplo, podemos usar métodos paramétricos para dados normalmente distribuídos, enquanto métodos não paramétricos podem ser empregados para dados não normais ou distorcidos. Sempre considere cuidadosamente a escolha do método para garantir a validade e a confiabilidade dos resultados.

Teste Z de duas amostras

Normalmente, os testes de hipóteses a serem realizados no teste ab compreendem um tamanho de amostra maior que 30, então vamos executar testes do tipo z assumindo uma distribuição normal.

Teste Z para proporções

Suponhamos que, para o exemplo analisado, tenhamos obtido as amostras necessárias para controle e tratamento, com tamanhos de 10.072 e 9.886, respectivamente. No grupo controle, 974 cliques foram feitos e, no grupo de tratamento, 1.242 cliques foram registrados. Vamos realizar o teste para essa situação: de statsmodels.stats.ratio import proportions_ztest, confint_proportions_2indep X_con = 974 #clicks control N_con = 10072 #impressions control X_exp = 1242 #clicks experimental N_exp = 9886 #impressions sucessos experimentais = [X_con, X_exp] nobs = [N_con, N_exp] z_stat, pval = proportions_ztest (sucessos, nobs=nobs) low_c, up_c = confint_proportions_2indep (X_exp, N_exp, X_con, N_con, compare='diff', alpha=alpha) print (estatística f'z: {z_stat: .2f} ') print (f'p-value: {pval: .3f}') print (f'ci 95% para a diferença: [{low_c: .3f}, {up_c: .3f}] ')

O valor de p é menor que o alfa predefinido de 0,05, o que significa que podemos rejeitar a hipótese nula e concluir que há uma diferença significativa entre os dois grupos. Um intervalo de confiança de [0,02, 0,038] para a diferença entre os dois CTRs também sugere que a verdadeira diferença entre os dois CTRs está dentro desse intervalo com um certo nível de confiança (95%). Como o intervalo não inclui 0 (e, portanto, o valor p é muito próximo de zero), que é o valor hipotético para nenhuma diferença entre os grupos, podemos concluir que há uma diferença estatisticamente significativa. Em outras palavras, rejeitamos a hipótese nula de que os CTRs são iguais e, em vez disso, aceitamos a hipótese alternativa de que os CTRs são diferentes.

Teste Z para meios

Se, em vez disso, nossa métrica for uma variável contínua, simularemos dois grupos de tamanho 60, onde a métrica pode obter valores aleatórios de uma distribuição normal de média 10 e desvio padrão 4 para ambos os grupos, e executaremos o teste: de statsmodels.stats.weightstats import ztest, zconfint N_con = 60 N_exp = 60 x_con = np.random.normal (10, 4, size =N_con) X_exp = np.random.normal (10, 4, size = N_exp) z_stat, pval = ztest (X_con, X_exp) low_c, up_c = zconfint (X_con, X_exp, alpha=alpha) print (estatística f'z: {z_stat: .2f} ') print (f'p-value: {pval: .3f}') imprimir (f'ci 95% para diferença: [{low_c: .3f}, {up_c: .3f}] ')

Nesse caso, como o valor de p é maior que alfa e os intervalos de confiança incluem zero, concluímos que não há diferença significativa entre as médias e aceitamos a hipótese nula.

Teste A/B com Bootstrapping

O bootstraping é uma técnica útil em testes A/B quando o tamanho da amostra é pequeno ou quando a distribuição subjacente dos dados é desconhecida. O bootstraping envolve a geração de várias amostras aleatórias com a substituição da amostra original para criar uma distribuição empírica das estatísticas da amostra. Isso pode ajudar a estimar a distribuição amostral da estatística de teste sem depender das suposições de normalidade e variância igual exigidas pelos métodos paramétricos tradicionais. def test_bootstrap (trmt, ctrl, N=1000): metric_diffs = [] mean_control = [] mean_treatment = [] # Repita o experimento N vezes para _ no intervalo (N): data_ctrl = ctrl.sample (frac=1.0, replace=true) data_trmt = trmt.sample (frac=1.0, replace=true) # Meça os valores médios metric_mean_ctrl = data_ctrl.mean () metric_mean_trmt = data_trmt.mean () # Meça a diferença das médias observadas_diff = metric_mean_trmt - metric_mean_ctrl metric_diffs.append (observed_diff) mean_control.append (metric_mean_ctrl) mean_treatment.append (metric_mean_trmt) obs_diff = trmt.mean () - ctrl.mean () standard_dev = np.array (metric_diff) .std () h_ = np.random.normal (0, standard_dev, np.array (metric_diffs) .shape) p_val = np.logical_or (np.array (h_) >= obs_diff, np.array (h_) <= -obs_diff) .mean () exp_dif = np.array (metric_diffs) .mean () left_i, right_i = np.percentile (np.array (metric_diffs), [5,95]) left_i, right_i = round (left_i,3), round (right_i,3) exp_dif = round (exp_dif, 3) print (f'p-value (trmt==ctrl): {p_val: .3f} ') print (f'expected dif (trmt-ctrl): {exp_dif: .2f}') print (f'ci 95% para diferença: [{left_i: .3f}, {right_i: .3f}] ') # Distribuição gráfica dos meios de controle e tratamento boot_gr = pd.DataFrame ({"control”: mean_control, “treatment”: mean_treatment}) boot_gr.plot (kind='kde') plt.show () # Também podemos ver a diferença como um gráfico dist aqui boot_gr = pd.DataFrame ({"equal_means”: h_, “diff_means”: metric_diffs}) boot_gr _gr.plot (kind='kde') plt.show () n = 100 x_CTRL = np.random.normal (4.5,3, n) x_TRMT = np.random.normal (5,3, n) teste_ bootstrap (série PD (X_trmt), série PD (x_CTRL))

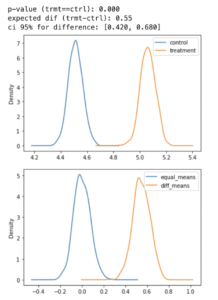
No exemplo simulado, geramos aleatoriamente duas distribuições normais, uma com média de 4,5 e outra com média de 5, com o mesmo desvio padrão de 3. O primeiro gráfico mostra as duas distribuições e podemos ver que há uma diferença real entre elas. No segundo gráfico, observamos duas distribuições. Uma distribuição é centrada em zero, correspondendo à hipótese nula se as médias forem iguais. A distribuição laranja representa a diferença entre tratamento e controle obtidos pelo bootstrapping. Conforme mostrado no gráfico, há uma diferença de 0,5. O valor p calculado e os intervalos de confiança apoiam a decisão de rejeitar a hipótese nula

Resultados possíveis: casos de intervalo de confiança

Quando calculamos a diferença entre os dois grupos e elaboramos os intervalos de confiança, podemos encontrar resultados diferentes. O gráfico a seguir mostra os intervalos de confiança em relação a um nível de significância prática (dmin) estabelecido em 0,02.

Conclusões

Concluindo, o teste A/B é uma ferramenta poderosa para empresas e indivíduos que desejam otimizar seus produtos digitais e campanhas de marketing. Ao usar métodos estatísticos para testar diferentes variáveis e designs, podemos obter informações valiosas sobre o que funciona e o que não funciona. É importante lembrar que o teste A/B não é uma correção única, mas um processo contínuo que exige testes e iterações contínuos. Escolhendo cuidadosamente nossos tamanhos de amostra, usando testes estatísticos apropriados e considerando as limitações e suposições de nossos experimentos, podemos tomar decisões baseadas em dados que, em última instância, levam a melhores experiências do usuário, maiores conversões e maior sucesso. Se você estiver interessado em saber mais sobre ciência de dados e aprendizado de máquina, fique à vontade para conferir nossos artigos detalhados sobre: https://blog.marvik.ai/

Referências

- Rosner, B. Fundamentos da Bioestatística (7ª ed.) - Curso Udacity: testes A/B. https://www.udacity.com/course/ab-testing--ud257 - Tatev Karen Aslanyan, guia completo para projeto, implementação e armadilhas de testes A/B. https://towardsdatascience.com/simple-and-complet-guide-to-a-b-testing-c34154d0ce5a