Introducción

¿Es propietario de una empresa o un profesional de TI? Si es así, es probable que siempre estés buscando formas de mejorar tu producto, servicio o algoritmo. Los cambios pueden ser riesgosos, especialmente en entornos productivos. Es difícil predecir si beneficiarán a su empresa. Aquí es donde las pruebas A/B se vuelven valiosas. Las pruebas A/B son una herramienta poderosa. Te permite probar diferentes versiones de tu producto, servicio o algoritmo. Esto ayuda a identificar si un cambio tendrá un impacto positivo. Las pruebas A/B utilizan la teoría de la probabilidad para respaldar la toma de decisiones basada en datos. Esto puede generar una mejor participación, tasas de conversión más altas y mayores ingresos. En este blog, exploraremos los conceptos básicos de las pruebas A/B, cubriendo conceptos y métodos estadísticos importantes. Empezaremos por analizar la importancia de seleccionar el tamaño de muestra adecuado. Utilizaremos el modelo de estadísticas biblioteca para calcular el tamaño de la muestra para proporciones y medias. Luego profundizaremos en la realización de una prueba z para determinar proporciones y medias, y exploraremos cómo usar el arranque para las pruebas A/B. Por último, analizaremos algunos de los posibles resultados de las pruebas A/B y cómo interpretarlos.

Prueba de latencia en Google

En 2009, Google realizó una prueba A/B para estudiar cómo la latencia de los sitios web afecta al comportamiento de los usuarios. Para esta prueba, Google dividió el tráfico de usuarios de forma aleatoria en dos grupos. Un grupo vio las páginas que se cargaron a una velocidad normal. El otro grupo vio páginas que tenían un retraso deliberado de 100 a 400 milisegundos. Los resultados de las pruebas fueron sorprendentes. Incluso un pequeño retraso de solo 100 milisegundos provocó una disminución apreciable en la participación de los usuarios. El grupo que experimentó el retraso en las páginas obtuvo un rendimiento entre un 0,2% y un 0,6% inferior en varias métricas de participación de los usuarios. Entre ellas figuraban las consultas de búsqueda y los clics en los anuncios. Estos hallazgos hicieron que Google se diera cuenta de que la latencia del sitio web afecta significativamente a la participación de los usuarios. Incluso las pequeñas mejoras en la velocidad de la página pueden mejorar considerablemente el comportamiento de los usuarios. La industria tecnológica ahora acepta ampliamente esta idea. Muchas empresas ahora invierten mucho en optimizar el rendimiento de sus sitios web y aplicaciones. Esto mejora la participación y la retención de los usuarios.

Un ejemplo práctico del proceso

Consideremos un ejemplo práctico. Supongamos que tiene un producto digital, como un sitio web. Quieres comprobar si un nuevo diseño para tu página de destino mejorará las conversiones o las tasas de clics. Las variables que consideres dependerán de tu aplicación empresarial específica. Los dos tipos comúnmente identificados son binarios o continuos. Las variables binarias pueden representar si un usuario ha instalado una aplicación o no. Se utilizan para calcular las tasas de conversión (proporciones). Las variables continuas se pueden asociar a un promedio, como el costo por clic. En este ejemplo, comprobaremos si la nueva página de destino mejora las tasas de clics (CTR). Sin embargo, consideraremos ambos casos para el resto del blog.

Ejecución de una prueba A/B

Para realizar una prueba A/B, primero debe definir dos grupos: tratamiento y control. A continuación, asignas individuos a cada grupo de forma aleatoria. El tamaño de cada grupo no es trivial y lo discutiremos más adelante. El grupo de tratamiento recibe la variante que se va a analizar, mientras que el otro grupo permanece igual. Mientras se ejecuta el experimento, es fundamental supervisar no solo la métrica principal que deseas optimizar, como el CTR. También debes prestar atención a otras métricas relevantes que deben mantenerse consistentes. Esto garantiza que cualquier cambio realizado para mejorar la métrica principal no afecte negativamente a otras métricas clave. Una vez que hayas recolectado las muestras, debes analizar los resultados de la prueba A/B. Al observar los resultados, vemos que el grupo de tratamiento obtuvo una puntuación un 1% más alta que el grupo de control. Al principio, esto puede parecer un resultado positivo. Sin embargo, es crucial garantizar que este resultado sea estadísticamente significativo. La significación estadística ayuda a cuantificar si un resultado es probable que se deba al azar o a un factor de interés. Al analizar los resultados de un experimento con una muestra, es posible que un grupo parezca superar al otro por casualidad. Sin embargo, es posible que este no sea el caso. Para evitar sacar conclusiones falsas comparando dos valores absolutos, realizamos una prueba de hipótesis. Esto nos permite concluir con cierta confianza que los resultados obtenidos no se deben únicamente al azar.

Por qué hacer pruebas de hipótesis

«Las pruebas de hipótesis proporcionan un marco objetivo para tomar decisiones utilizando métodos probabilísticos, en lugar de basarse en impresiones subjetivas. Las personas pueden formarse opiniones diferentes al analizar los datos, pero una prueba de hipótesis proporciona un criterio de toma de decisiones uniforme que es coherente para todas las personas». - Rosner, B. Fundamentos de bioestadística.

En las pruebas A/B, probaremos si hay un cambio significativo en nuestra métrica después de implementar la variante y también la magnitud del efecto. Por lo general, formularemos hipótesis de los siguientes tipos:

• Hipótesis nula (H0): La métrica es la misma para ambos grupos. Es decir, mean_treatment = mean_control.
• Hipótesis alternativa (H1): La métrica es diferente. Es decir, mean_treatment! = control medio

El proceso

El procedimiento estándar para la prueba de hipótesis es definir las hipótesis nulas y alternativas. Luego determinamos si apoyamos o rechazamos la hipótesis nula. Para ello, calculamos una estadística de prueba. Esto mide qué tan lejos está la estimación de la muestra del valor hipotético bajo la hipótesis nula. En este contexto, mide qué tan lejos está de cero la diferencia calculada entre los dos grupos. Esto se debe a que la hipótesis nula es que la métrica es la misma para los dos grupos. A continuación, utilizamos la estadística de prueba para calcular el valor p. Esto representa la probabilidad de observar el resultado si la hipótesis nula es verdadera. En otras palabras, representa la probabilidad de obtener una diferencia como la observada. Esto supone que la métrica es la misma para ambos grupos. Si el valor p es inferior a un cierto nivel de significancia (también conocido como alfa), entonces rechazamos la hipótesis nula en favor de la hipótesis alternativa. Cuanto más bajo sea el valor p, menos probable es que los resultados se deban únicamente al azar. Sin embargo, si el valor p es mayor o igual que el nivel de significancia, no rechazamos la hipótesis nula. Esto indica que no hay suficiente evidencia para concluir que los grupos o variables son diferentes.

Posibles resultados

Todos los resultados de una situación de prueba de hipótesis generalmente se refieren a la hipótesis nula. Por lo tanto, si decidimos que H0 es verdadera, decimos que aceptamos H0. Si decidimos que H1 es verdadera, decimos que H0 no es verdadera o, de manera equivalente, que rechazamos H0. Por lo tanto, hay cuatro resultados posibles:

- Rosner, B. Fundamentos de bioestadística (7ª ed.), pág. 204

Idealmente, queremos aceptar H0 siempre que sea realmente cierto y rechazarlo en caso contrario. En este contexto de toma de decisiones en condiciones de incertidumbre, podemos cometer dos tipos de errores. Esto se debe a que estamos trabajando con una muestra y queremos comprobar si estos resultados pueden extrapolarse a la población.

Tipos de errores

• Error de tipo 1: Rechazar H0 cuando es cierto. Alfa (α) representa la probabilidad de cometer un error de tipo 1, también conocido como falso positivo. Lo mencionamos anteriormente al definir el umbral en el que rechazamos o no rechazamos la hipótesis nula.
• Error de tipo 2: Aceptar H0 cuando es falso. Beta (β) representa la probabilidad de cometer un error de tipo 2, también llamado falso negativo.

El resultado que más nos interesa en este contexto es la elección de H1 cuando es realmente cierto. La probabilidad asociada se denomina potencia estadística y se denota con 1 − β. La potencia de una prueba de hipótesis es la probabilidad de que la prueba rechace correctamente la hipótesis nula. Es una medida de la probabilidad, dado un tamaño de muestra determinado, de detectar una diferencia estadísticamente significativa cuando la hipótesis alternativa es cierta. Una potencia baja indica una probabilidad baja de detectar una diferencia significativa, incluso si existen diferencias reales entre los grupos de control y experimental.

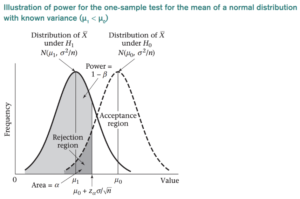
- Rosner, B. Fundamentos de bioestadística (7ª ed.), pág. 222.

Cuando diseñamos un experimento, normalmente establecemos valores para alfa, beta (y potencia). Pero también necesitamos definir qué cambios esperamos ver entre los dos grupos. ¿Qué cambio importará en este caso en particular? Esto se denomina significación práctica o también se conoce como tamaño del efecto deseado. Estos tres factores: alfa, potencia y tamaño del efecto están directamente relacionados con el tamaño de la muestra. La relación entre ellos es compleja e interdependiente. Es un concepto muy importante de entender.

El tamaño de la muestra y su importancia

El tamaño de la muestra desempeña un papel fundamental en las pruebas de hipótesis. Afecta a los valores de alfa, beta y potencia. El aumento del tamaño de la muestra generalmente reduce tanto la alfa como la beta, al tiempo que aumenta la potencia. Esto se debe a que un tamaño de muestra más grande proporciona más datos y reduce el error de muestreo. Esto facilita la detección de un efecto verdadero, si es que existe. Como resultado, un tamaño de muestra más grande generalmente conduce a una estimación más precisa de los parámetros de la población. Esto, a su vez, aumenta la potencia de la prueba. Por otro lado, la disminución del tamaño de la muestra generalmente aumenta tanto el alfa como el beta, al tiempo que disminuye la potencia. Esto se debe a que con un tamaño de muestra más pequeño, hay una mayor probabilidad de que la variación aleatoria afecte a los resultados. Esto puede llevar a una conclusión falsa positiva o falsa negativa. Como resultado, un tamaño de muestra más pequeño puede disminuir la precisión de la estimación. Esto, a su vez, reduce la potencia de la prueba. El tamaño del efecto afecta directamente al tamaño de la muestra. Un tamaño de efecto mayor generalmente requiere un tamaño de muestra más pequeño para lograr el mismo nivel de potencia. Por el contrario, un tamaño de efecto más pequeño requerirá un tamaño de muestra más grande para lograr el mismo nivel de potencia. El tamaño del efecto se puede considerar como la magnitud de la diferencia entre los grupos que se comparan. Por lo general, se mide utilizando medidas estandarizadas del tamaño del efecto, como la d de Cohen.

Alfa, potencia y tamaño del efecto en las pruebas A/B

Gráfico de alfa, beta y potencia en el caso de un tamaño de muestra pequeño frente a un tamaño de muestra grande para un mismo tamaño de efecto de 0.02:

Tenga en cuenta que si aumentamos el tamaño del efecto, por ejemplo, de 0.02 a 0.1, el centro de las distribuciones estaría más separado, ya que la distancia entre 0 (el caso de la hipótesis nula en la que los grupos tienen la misma métrica) y 0.1 es mucho mayor que entre 0 y 0.02, tendríamos menos error y necesitaríamos menos datos. Esto significa que un tamaño de efecto mayor puede conducir a resultados estadísticamente más significativos con un tamaño de muestra más pequeño. También es importante tener en cuenta la importancia práctica del tamaño del efecto, ya que un tamaño de efecto muy pequeño puede no ser significativo, incluso si es estadísticamente significativo. El tamaño del efecto indica qué diferencia es relevante en términos comerciales y cuantifica qué cambio es importante que se produzca.. Depende del experimento que se esté realizando. No ocurre lo mismo en un contexto médico, por ejemplo, en el que comprobamos si un nuevo medicamento mejorará los resultados de los pacientes, que cuando evaluamos si cambiar una función de un sitio web mejorará las conversiones. En el primer caso, una diferencia del 5 al 10% puede considerarse prácticamente significativa, porque si el cambio es muy pequeño, no vale la pena el coste de introducir un nuevo medicamento. Por otro lado, en este último caso, una diferencia del 1 al 2% puede ser relevante cuando hablamos de miles de usuarios, por lo que valdría la pena implementar el cambio. En general, la relación entre el tamaño del efecto y el tamaño de la muestra resalta la importancia de considerar cuidadosamente la cuestión de investigación y la magnitud del efecto que se está estudiando al diseñar los experimentos.

¿Cómo elegir el tamaño de la muestra en las pruebas A/B?

Determinar el tamaño de la muestra es uno de los pasos más importantes para diseñar una prueba A/B. Un tamaño de muestra demasiado pequeño puede llevar a resultados poco concluyentes, mientras que un tamaño de muestra demasiado grande puede desperdiciar recursos. Por lo tanto, es importante elegir un tamaño de muestra adecuado para la prueba A/B. Como se mencionó anteriormente, el tamaño de la muestra requerido para una prueba de hipótesis depende de varios factores, como el tamaño del efecto que se espera observar, el nivel de significancia deseado, la potencia de la prueba, el tipo de prueba estadística utilizada y la variabilidad de los datos. Primero importemos la biblioteca import statsmodels.stats.api como nivel de significancia de sms: esto es lo que antes llamábamos alfa, un nivel de significancia normalmente se establece en un valor predeterminado (como 0,05 o 0,01) y se usa en las pruebas de hipótesis para determinar si se rechaza o no se rechaza la hipótesis nula. alpha = 0.05 Significación práctica: también conocida como tamaño del efecto, si nuestra variable es una proporción y queremos observar si nuestro CTR va de 0.10 a 0.15, usaremos la función proportion_effectsize para obtener el valor correspondiente. effect_size = sms.proportion_effectsize (0.10, 0.15) Si nuestra variable es una media y queremos ver si cambia un 5%, también debemos tener en cuenta la desviación estándar de la distribución a partir de la cual estamos estimando, esta desviación se puede calcular en función de una muestra de la población en estudio. std= 0.53 effect_size = 0.05/std Potencia: Se suele establecer un valor de 0.8 como umbral para power. power = 0.8 Finalmente calculamos el tamaño de muestra requerido como: required_n = sms.normalindPower () .solve_power (effect_size, power=power, alpha=alpha)

Factores que afectan el tamaño de la muestra

1. A medida que aumenta la desviación estándar, también aumenta el tamaño de muestra requerido.
2. Reducir el nivel de significancia (decreciente α) conducirá a un aumento en el tamaño de la muestra.
3. Si la potencia requerida (1 − β) aumenta, esto también provocará un aumento en el tamaño de la muestra.
4. El aumento de la distancia absoluta entre la media nula y la alternativa (|µ0 − µ1| -> tamaño del efecto) provoca una disminución en el tamaño de la muestra.

El éxito de una prueba A/B depende de la calidad del diseño del experimento, la precisión de los datos recopilados y el rigor del análisis estadístico. Por lo tanto, asegúrese de planificar y ejecutar cuidadosamente cada paso de la prueba para lograr resultados significativos que puedan informar su toma de decisiones.

Prueba de hipótesis

Una vez hayamos recolectado todas las muestras que definamos como necesarias para realizar la prueba, procederemos a ejecutarla. Para ello existen diferentes opciones: La prueba de hipótesis se puede realizar utilizando ambas métodos paramétricos, que asumen una distribución subyacente, como la prueba z y la prueba t, o métodos no paramétricos, que no hacen suposiciones sobre las distribuciones, como la prueba exacta de Fisher, la prueba Chi-Squared o la prueba de suma de rangos de Wilcoxon/Mann Whitney. Tenga en cuenta que la elección entre métodos paramétricos o no paramétricos depende de los datos que se analicen y de las suposiciones que podamos hacer sobre la población subyacente. Por ejemplo, podemos usar métodos paramétricos para datos distribuidos normalmente, mientras que los métodos no paramétricos se pueden emplear para datos no normales o asimétricos. Considere siempre cuidadosamente la elección del método para garantizar la validez y confiabilidad de los resultados.

Prueba Z de dos muestras

Por lo general, las pruebas de hipótesis que se realizarán en las pruebas ab comprenden un tamaño de muestra superior a 30, por lo que vamos a ejecutar pruebas de tipo z asumiendo una distribución normal.

Prueba Z para proporciones

Supongamos que para el ejemplo analizado, obtuvimos las muestras necesarias para el control y el tratamiento, con tamaños de 10,072 y 9,886, respectivamente. En el grupo de control, se realizaron 974 clics, y en el grupo de tratamiento, se registraron 1.242 clics. Realicemos la prueba para esta situación: from statsmodels.stats.proportion import proportions_ztest, confint_proportions_2indep x_con = 974 #clicks control N_con = 10072 #impressions control x_exp = 1242 #clicks experimental N_exp = 9886 #impressions éxitos experimentales = [x_con, x_exp] nobs = [N_con, N_exp] z_stat, pval = proportions_ztest (éxitos, nobs=nobs) low_c, up_c = confint_proportions_2indep (x_exp, n_exp, x_con, n_con, compare='diff', alpha=alpha) print (f'z statistics: .2f} ') print (f'p-value: {pval: .3f}') print (f'ci por diferencia: [{low_c: .3f}, {up_c: .3f}] ')

El valor p es menor que el alfa predefinido de 0.05, lo que significa que podemos rechazar la hipótesis nula y concluir que hay una diferencia significativa entre los dos grupos. Un intervalo de confianza de [0,02, 0,038] para la diferencia entre los dos CTR también sugiere que la diferencia real entre los dos CTR se encuentra dentro de este rango con un cierto nivel de confianza (95%). Como el intervalo no incluye 0 (y, por lo tanto, el valor p está muy cerca de cero), que es el valor hipotético de que no hay diferencia entre los grupos, podemos concluir que existe una diferencia estadísticamente significativa. En otras palabras, rechazamos la hipótesis nula de que los CTR son iguales y, en cambio, aceptamos la hipótesis alternativa de que los CTR son diferentes.

Prueba Z para determinar los medios

Si, por el contrario, nuestra métrica es una variable continua, simularemos dos grupos de tamaño 60, donde la métrica puede tomar valores aleatorios de una distribución normal de media 10 y desviación estándar 4 para ambos grupos, y ejecutaremos la prueba: from statsmodels.stats.weightstats import ztest, zconfint N_con = 60 N_exp = 60 x_CON = np.random.normal (10, 4, size =N_con) x_CON exp = np.random.normal (10, 4, size = N_exp) z_stat, pval = ztest (x_CON, x_EXP) low_c, up_c = zconfint (x_CON, x_EXP, alpha=alpha) print (estadística f'z: {z_stat: .2f} ') print (f'p-value: {pval: .2f}') print (f'p-value: .pval: .2f} ') print (f'p-value: .pval: .2f}') print (f'p-value: .pval: .2f} ') print (f'p-value: .pval: .2f}') print (f'p-value: .pval: .2f} ') print (f'p-value: 3f}') print (f'ci 95% para diferencia: [{low_c: .3f}, {up_c: .3f}] ')

En este caso, dado que el valor p es mayor que alfa y los intervalos de confianza incluyen cero, concluimos que no hay una diferencia significativa entre las medias y aceptamos la hipótesis nula.

Pruebas A/B con Bootstrapping

El arranque es una técnica útil en las pruebas A/B cuando el tamaño de la muestra es pequeño o cuando se desconoce la distribución subyacente de los datos. El arranque implica generar varias muestras aleatorias sustituyéndolas por la muestra original para crear una distribución empírica de las estadísticas de la muestra. Puede ayudar a estimar la distribución muestral de la estadística de prueba sin basarse en los supuestos de normalidad e igualdad de varianza requeridos por los métodos paramétricos tradicionales. def test_bootstrap (trmt, ctrl, N=1000): metric_diffs = [] mean_control = [] mean_treatment = [] # Repita el experimento N veces para _ in range (N): data_ctrl = ctrl.sample (1.0, replace=True) data_trmt = trmt.sample (frac=1.0, replace=True) # Valores medios de medición metric_mean_ctrl = data_ctrl.mean () metric_mean_trmt = data_trmt.mean () # Mide la diferencia de los medios observados_diff = metric_mean_trmt - metric_mean_ctrl metric_diffs.append (observed_diff) mean_control.append (metric_mean_ctrl) mean_treatment.append (metric_mean_trmt) obs_diff = trmt.mean () - ctrl.mean () standard_dev = np.array (metric_diffs) .std () h_ = np.random.normal (0, standard_dev, np.array (metric_diffs) .shape) p_val = np.logical_or (np.array (h_) >= obs_diff, np.array (h_) <= -obs_diff) .mean () exp_dif = np.array (metric_diffs) .mean () left_i, right_i = np.percentile (np.array (metric_diffs), [5,95]) left_i, right_i = round (left_i,3), round (right_i,3) exp_dif = round (exp_dif, 3) print (f'p-value (trmt==ctrl): {p_val: .3f} ') print (f'expected dif (trmt-ctrl): {exp_dif: .2f}') print (f'ci 95% por diferencia: [{left_i: .3f}, {right_i: .3f}] ') # Represente gráficamente la distribución de los medios de control y tratamiento _gr = pd.DataFrame ({"control»: mean_control, «treatment»: mean_treatment}) boot_gr.plot (kind='kde') plt.show () # También podemos ver la diferencia como un diagrama de distribución aquí boot_gr = pd.DataFrame ({"equal_means»: h_, «diff_means»: metric_diffs}) boot_gr.frame ({"equal_means»: metric_diffs}) boot_gr.frame ({"equal_means»: h_, «diff_means»: metric_diffs}) boot_gr.frame ({"equal_means»: metric_diffs}) boot_gr.frame ({"equal_means»: h_, «diff_means»: metric_diffs .plot (kind=' kde') plt.show () n = 100 x_CTRL = np.random.normal (4.5,3, n) x_TRMT = np.random.normal (5,3, n) test_ bootstrap (serie PDF (x_TRMT), serie PDF (x_Ctrl))

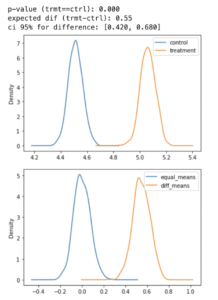
En el ejemplo simulado, generamos aleatoriamente dos distribuciones normales, una con una media de 4,5 y la otra con una media de 5, con la misma desviación estándar de 3. La primera gráfica muestra ambas distribuciones y podemos ver que hay una diferencia real entre ellas. En la segunda gráfica, observamos dos distribuciones. Una distribución está centrada en cero, lo que corresponde a la hipótesis nula si las medias fueran iguales. La distribución naranja representa la diferencia entre el tratamiento y el control obtenida mediante el arranque. Como se muestra en la gráfica, hay una diferencia de 0,5. El valor p y los intervalos de confianza calculados respaldan la decisión de rechazar la hipótesis nula

Posibles resultados: casos de intervalo de confianza

Cuando calculamos la diferencia entre los dos grupos y elaboramos los intervalos de confianza sobre ella, podemos encontrar resultados diferentes. La siguiente gráfica muestra los intervalos de confianza con respecto a un nivel de significación práctica (dmin) establecido en 0.02.

Conclusiones

En conclusión, las pruebas A/B son una herramienta poderosa para las empresas y las personas que desean optimizar sus productos digitales y campañas de marketing. Al utilizar métodos estadísticos para probar diferentes variables y diseños, podemos obtener información valiosa sobre lo que funciona y lo que no. Es importante recordar que las pruebas A/B no son una solución única, sino un proceso continuo que requiere pruebas e iteraciones continuas. Al elegir cuidadosamente los tamaños de nuestras muestras, utilizar las pruebas estadísticas adecuadas y tener en cuenta las limitaciones y los supuestos de nuestros experimentos, podemos tomar decisiones basadas en los datos que, en última instancia, conducen a una mejor experiencia de usuario, mayores conversiones y un mayor éxito. Si está interesado en obtener más información sobre la ciencia de datos y el aprendizaje automático, no dude en consultar nuestros artículos detallados sobre: https://blog.marvik.ai/

Referencias

- Rosner, B. Fundamentos de bioestadística (7ª ed.) - Curso de Udacity: pruebas A/B. https://www.udacity.com/course/ab-testing--ud257 - Tatev Karen Aslanyan, Guía completa sobre el diseño, la implementación y las dificultades de las pruebas A/B. https://towardsdatascience.com/simple-and-complet-guide-to-a-b-testing-c34154d0ce5a