La eficiencia desempeña un papel fundamental en muchas industrias, desde la logística y la fabricación hasta la gestión de recursos y más. Problemas como la optimización de las rutas de entrega, la programación de tareas o la asignación de recursos han adquirido una gran relevancia en nuestra vida diaria, debido principalmente al aumento masivo del comercio electrónico minorista en los últimos dos años.

A pesar de no estar tan de moda como la IA, y como mencionamos en nuestra última entrada Introducción a la programación lineal de números enteros mixtos (MILP), las soluciones de optimización no solo pueden ahorrar millones a las empresas, sino que también pueden estar estrechamente relacionadas con la satisfacción del cliente, ya que permiten que los productos se muevan de manera eficiente de los productores a los consumidores. La desventaja de ejecutar una optimización a gran escala es que exige mucho recursos informáticos, especialmente si se ejecuta con muchas variables y restricciones. Por ejemplo, se cree que las entregas aumentarán un 80% de aquí a 2027, lo que desafía la capacidad de las soluciones basadas en CPU para responder a esta demanda.

En este blog analizamos NVIDIA CuOpt, un microservicio innovador de optimización de la IA que se especializa en la toma de decisiones óptimas en problemas a gran escala con millones de variables y restricciones al proporcionar soluciones aceleradas por GPU, casi en tiempo real.

Acerca de CuOpt

Presentaremos CuOpt de la misma forma en que consultaría su LLM preferido.

¿Qué es?

NVIDIA CuOpt es un motor de optimización lineal y combinatoria acelerado por GPU para resolver problemas complejos de optimización de rutas, como el enrutamiento de vehículos y la programación lineal de gran tamaño. NVIDIA CuOpt está disponible como un microservicio de IA.

¿Qué entendemos por CuOpt como microservicio de IA?

NVIDIA se refiere a CuOpt como un microservicio de IA de forma genérica, pero la forma más fácil (y rápida) de entender cómo acceder a él es explorar la demostración basada en la API y ejecutar solicitudes a la API gestionada mediante un token NGC (de momento, 1000 créditos gratis con tu cuenta de usuario gratuita de NGC). A través de una cuenta NGC de NVIDIA, también es posible implementar un contenedor específico de Cuopt, ya sea alojándolo en el hardware que elija o implementándolo, por ejemplo, en AWS Marketplace o Azure Marketplace. También está disponible la biblioteca cuopt-thin-client para Python. Todo esto está implícito en el concepto de «microservicio de IA» de CuOpt.

¿Qué ofrece?

CuOpt ofrece soluciones logísticas aceleradas por GPU basadas en heurísticas, metaheurísticas y optimizaciones para calcular problemas complejos con una amplia gama de variables y restricciones.

¿Su mayor valor? Su precisión récord mundial: en marzo de 2024, NVIDIA anunció que CuOpt ocupaba el primer puesto en el 100% de los índices de referencia de enrutamiento más importantes de los tres años anteriores.

¿Qué puedo solucionar con CuOpt?

Los espacios problemáticos típicos incluyen:

• El problema del vendedor ambulante (TSP)
• Problema de enrutamiento de vehículos (VRP)
• Problema de recogida y entrega (PDP)
• Programación lineal (LP)
• Programación lineal de enteros mixtos (MILP)

Descargo de responsabilidad: Por el momento, LP y MILP son funciones de acceso anticipado y actualmente solo están disponibles para clientes selectos. Por lo tanto, por el momento, nos centramos en probar un ejemplo de optimización de rutas, específicamente el caso práctico de entrega en la última milla, en el que se presenta el problema de enrutamiento de vehículos.

No obstante, es importante destacar que el Las funciones LP y MILP muestran el mayor potencial, ya que son algunos de los problemas de optimización más comunes en la industria. Esperamos que nuestros conocimientos sobre el uso del VRP se puedan transferir a LP y MILP una vez que esté completamente disponible.

Problema de optimización de Last Mile Delivery

La entrega de última milla (LMD) es la fase final del proceso de entrega. Algunos ejemplos prácticos de posibles escenarios en los que sería necesario optimizar la entrega en última milla son los vehículos de reparto autónomos, la entrega desde el restaurante al cliente a través de conductores independientes y la compra y entrega de pedidos en línea. Como problema de optimización, se trata de un caso particular del problema de generación de rutas para vehículos. De hecho, como también se mencionó en nuestra entrada anterior del blog Introducción a la programación lineal de números enteros mixtos (MILP), la optimización del enrutamiento pertenece a la familia de problemas de optimización MILP.

Como cualquier problema de optimización, LMD se presenta con una función objetivo, que es la siguiente:

c_ij: Coste del viaje de i a j

x_vij: Variable de decisión binaria que indica si el vehículo v viaja de i a j

La solución optimizada para esta función objetiva proporciona la ruta de tareas óptima para cada vehículo, lo que minimiza los costos totales de entrega, teniendo en cuenta todas las especificaciones/restricciones siguientes:

• Los vehículos #V deben completar las tareas #T en diferentes ubicaciones,
• #L es el universo de los lugares,
• {{c_ij}} es la matriz de costos (al cuadrado) con el costo de «distancia» conocido entre todas las ubicaciones i, j.
  • Si se mide a través de la distancia física en kilómetros, hay una matriz de costos para todos los vehículos
  • Si se mide a través del precio de la gasolina entre las ubicaciones, la matriz de costos sería específica del vehículo.
• {{t_ij}} es la matriz de tiempo y costo (también cuadrada), que especifica cuánto tiempo se tarda en llegar a cada ubicación i, j,
• Cada vehículo tiene una restricción de capacidad C específica (como las dimensiones de peso o volumen de un camión),
• Cada tarea implica demandas de capacidad específicas (por ejemplo, el peso y el tamaño del paquete),
• Cada vehículo debe operar dentro de un período de tiempo específico (por ejemplo, las horas de trabajo del conductor),
• Todos los vehículos pueden tomar descansos de una duración determinada, tomados dentro de un período de tiempo específico (por ejemplo, la pausa de 30 minutos para comer del trabajador),
• Y dado un período de tiempo específico en el que se debe realizar la tarea

Si se resuelven manualmente, estas restricciones se modelarían matemáticamente junto con otras restricciones de conservación del flujo.

Sin embargo, CuOpt no exige el modelo matemático del problema. Solo requiere cargar las especificaciones en el esquema de la carga útil.

Entrega de última milla con CuOpt

¿Cómo interpretar las especificaciones del LMD para la carga útil de CuOpt?

Fácil. Simplemente rellena los campos de la carga útil. La mayoría de ellos se explican por sí mismos, como «vehicle_ids», «task_locations» o «task_duration». En esta sección analizaremos la carga útil predeterminada proporcionada en Demostración de la API CuOpts , que también se encuentra al final de esta entrada de blog, en la sección Apéndice: Ejemplo de carga útil de CuOpt.

En estas directrices, resumimos nuestras ideas sobre cómo se modela el LMD y todas sus restricciones se ajustan a la carga útil de la API de CuOpt:

1. El primer nivel de la carga útil tiene 3 claves: action, data y client_version.
   1. «acción»: «CUOPT_OptimizedRouting» informa a CUOpt de que el problema abordado es para la optimización del enrutamiento. El valor CuOPT_LP con un diferente dato el campo se utilizaría si la función de programación lineal estuviera disponible. Nota: La respuesta actual de la API con CuOPT_LP is 422 — «NVIDIA CuOpt: la programación lineal está deshabilitada».
   2. «datos»: {...} este campo contiene toda la información relevante del problema de optimización. En el caso de la optimización de rutas, esto incluye las matrices de costes y tiempos, las restricciones de vehículos y flotas, las restricciones de tareas y la configuración del solucionador.
   3. «client_version» apunta de forma predeterminada a una versión de API válida y casi no se utiliza.
2. «cost_matrix_data»: {«datos»: {«0»: [<the matrix>]}} se usaría si se puede suponer que los datos de cost_matrix son los mismos para todos los vehículos.
3. «cost_matrix_data»: {«datos»: {«1»: [<one matrix>], «2»: [
   1. 1. , traducida a través del coste: 1 campo. Esto significa que la función objetivo minimizará los costos. Si hubiera tiempo_viaje: 1 en cambio, entonces la función objetivo se definiría como
   ]}} es la sintaxis utilizada en el ejemplo de carga útil que aparece a continuación y significa que hay dos vehículos, cada uno con matrices de costes diferentes.
4. La analogía de los puntos 2) y 3) también se aplica a la datos_matrix_temporales.
5. Las matrices de tiempo y costo deben cuadrarse. Sus dimensiones vienen dadas por el número de ubicaciones del problema. Las ubicaciones se obtienen uniendo las ubicaciones de los depósitos y las ubicaciones de las tareas.
   1. En el ejemplo, hay 3 ubicaciones: 0, 1 y 2 después de las filas/columnas de las matrices de tiempo y costo.
   2. El datos_de flota campo de ubicaciones de vehículos se refiere al punto de partida/depósito de cada vehículo. Para ambos vehículos, el punto de partida es la ubicación 0. Por motivos de dimensionalidad, las ubicaciones de cada vehículo se presentan como [0,0].
   3. El datos_tareas campo de ubicaciones de tareas se refiere a que las dos tareas del problema se encuentran en 1 y 2. Decimos que si un vehículo llega a la ubicación 1, entonces esa tarea está cubierta.
6. costos_máxicos_vehículo_tiempos/máximo_tiempo del vehículo siguen la misma lógica específica del vehículo. Son límites superiores específicos para el coste total y el tiempo total de viaje de cada vehículo.
7. Hay campos que hacen referencia a las ventanas de tiempo:
   1. El datos_de flota campo de ventanillas de tiempo del vehículo proporciona el intervalo de tiempo/ventana de tiempo de cada vehículo. En el ejemplo, hay 2 rangos que asocian cada ventana de tiempo a la misma cantidad de vehículos.
   2. El datos_tareas campo de tiempo_de_tareas_windows proporciona el intervalo en el que se debe realizar cada tarea. En el ejemplo, hay 2 rangos que asocian cada ventana de tiempo a la misma cantidad de ubicaciones de tareas.
8. El datos_de flota campos de tiempo_de_interrupción_ventanillas del vehículo, duraciones de rotura del vehículo y ubicaciones de rotura de vehículos se refieren al período, la duración y el lugar en los que se permite que el vehículo tome descansos. Por ejemplo, el conductor de un vehículo podría tomarse una pausa de 30 minutos para comer entre las 11 a. m. y las 2 p. m., y dejar el camión en un estacionamiento específico.
9. vehicle_order_match y order_vehicle_match asocie los vehículos que deben asistir a tareas específicas y las tareas a las que deben asistir vehículos específicos. Si no se iguala, esta restricción hará que el problema de optimización sea inmediatamente inviable.
10. capacidades y demandas son restricciones que se refieren a la capacidad del vehículo y a la demanda de capacidad de la tarea. Por ejemplo, si un mensajero en bicicleta puede transportar hasta 3 kg de paquetes (capacidad del vehículo) y cada paquete que va a entregar pesa 1 kg, el motorista no podrá realizar más de 3 tareas en su ruta. En el mismo escenario, si una tarea pesara 4 kg, el motorista no podría asistir y la tarea quedaría excluida.
    1. En el ejemplo proporcionado, hay tantas restricciones de capacidad como vehículos: 2 vehículos, 2 especificaciones de capacidad.
    2. En el ejemplo hay tantas especificaciones de demanda como tareas: 2 tareas, 2 especificaciones de demanda.
    3. Es posible tener varias dimensiones de capacidad/demanda, como el peso y el volumen, como también es el caso en el ejemplo de la carga útil. Decimos que hay una especificación de peso para cada vehículo, una especificación de volumen para cada vehículo, una especificación de peso para cada tarea y una especificación de volumen para cada tarea. Esto explica la capacidades y demandas dimensionalidad de la carga útil.
11. omite los primeros viajes (y drop_deturn_trips) simplemente determinan que el costo desde el almacén hasta la primera tarea (y desde la última tarea hasta el almacén) no debe tenerse en cuenta en la función objetivo. Este es el caso si, por ejemplo, aunque lo ideal es que la ruta termine de vuelta en el depósito, al conductor se le permite hacer recados personales en el vehículo de la empresa después del horario laboral.
12. El campo solver_config tiene la configuración correspondiente para el solucionador del modelo de optimización.
    1. límite de tiempo: 1 significa que el algoritmo debe iterar la optimización durante no más de 1 segundo. En las próximas secciones siguientes se abordará un análisis más profundo sobre la variación de este parámetro.
    2. El objetivos El campo define en qué debe centrarse la función objetivo. La definición actual de LMD se centra en

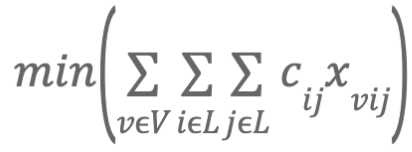
1. 1. optimizado para minimizar el tiempo de viaje.
   2. Lo mismo puede interpretarse con la varianza_tamaño_ruta y varianza_ruta_tiempo_servicio_de_ruta parámetros, en los que, si se establecen en valores distintos de cero, se tendrán en cuenta en la función objetivo.
   3. El premio campo es una lectura diferente de la función objetivo. Si se establece en un valor diferente de cero, tendría como objetivo maximizar una variable de premio que podría representar, por ejemplo, una comisión mediante un sistema de recompensas, beneficios netos, etc.

Información adicional: la carga útil de la programación lineal puede incluir el dato campo a maximizar: Bandera verdadera o falsa y un campo de tolerancia en el solver_config: {«tolerancias»: {«optimización»: 0.0001}} campo.

¿Qué pasa con el token necesario?

Señalemos que la guía anterior para mapear las variables del problema en la carga útil de CuOpt es útil independientemente de cómo utilice CuOpt, ya sea que esté utilizando la demostración de la API o la dependencia del cliente de Python.

Sin embargo, descubrimos que la forma más fácil de probarlo fuera de la demostración de la interfaz de usuario es:

1. Reutilizar el fragmento proporcionado en su propio entorno de Python.
2. Haga clic en el botón «Obtener clave de API» en la interfaz de usuario y siga los pasos para obtener un token.
3. Colocar el token en una variable de entorno a la que se pueda hacer referencia en el campo «Autorización» del encabezado, o en la elección del desarrollador sobre el uso de la variable de entorno.

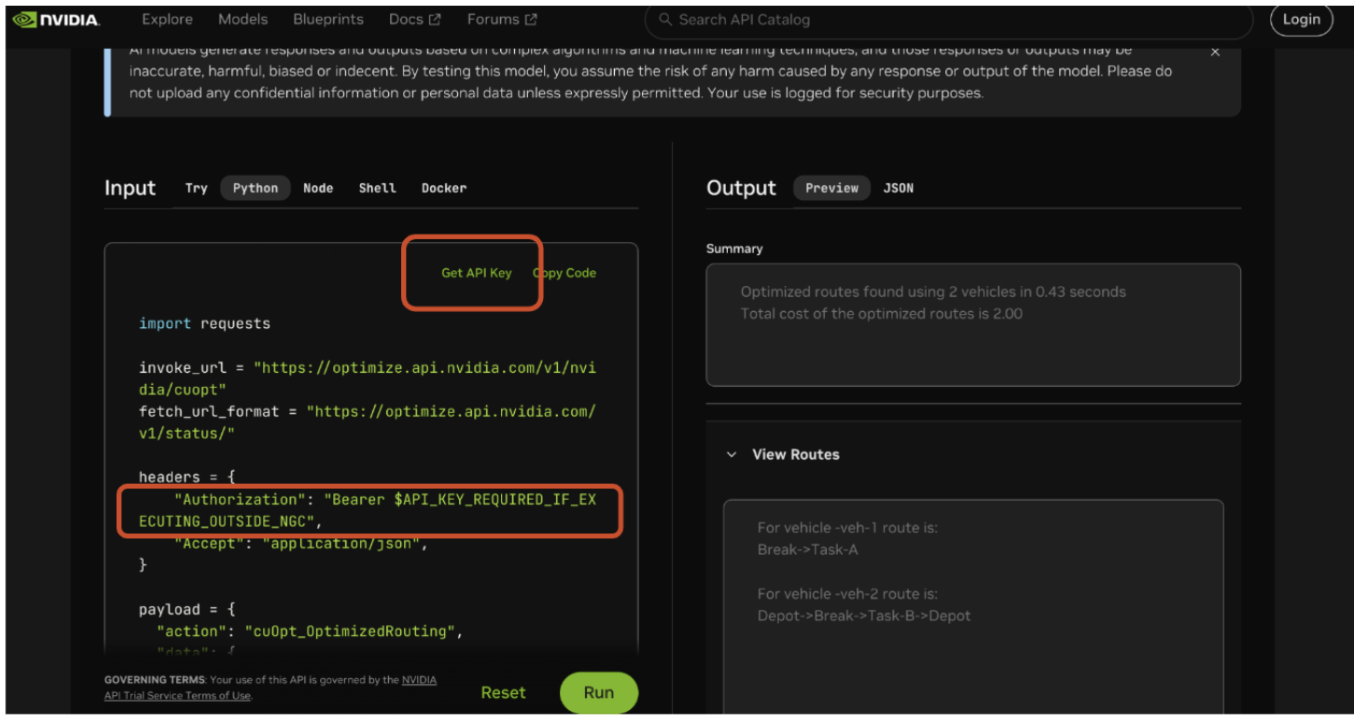
Interpretación de respuestas de API

La respuesta es mucho más sencilla que la carga útil: proporciona el número de vehículos utilizados en la solución óptima encontrada, el coste total de la función objetivo, la ruta de entrega de cada vehículo y si se abandonó alguna tarea.

La nota más relevante del cuerpo de la respuesta es que el campo «response» [«solver_response»] [«status»] puede ser:

• 0, lo que significa que se encontró una solución factible.
• 1, lo que significa que no hay una solución factible para el problema planteado.

Por ejemplo, la respuesta a la carga útil predeterminada está disponible en el sitio de demostración de la API de CuOpts y también se proporciona al final de esta entrada de blog, en la sección Apéndice: Carga útil de respuesta de CuOpt.

Si no es factible, la respuesta incluirá la información de la infracción de la restricción, lo que puede resultar muy útil.

Nota adicional: una solicitud solo puede gestionar una cantidad limitada

La letra pequeña de la documentación de referencia de la API nvidia/CuOpt para Enviar al punto final POST del solucionador establece lo siguiente:

«Si el tamaño de los datos supera los 250 KB, utilice la API de activos grandes para subirlos a s3. En esos casos, defina los datos como nulos e incluya el encabezado NVCF-INPUT-ASSET-REFERENCES: $ASSET_ID en la solicitud POST».

Por improbable que parezca que supere los 250 KB en el cuerpo de una solicitud POST, si se encuentra en esta situación, consulte la documentación de referencia de API de activos de NVCF donde se explica el uso de los puntos finales de lista, creación de activos, obtención de detalles de activos y eliminación de activos.

Problema ficticio de LMD: CuOpt y Pyomo

En esta sección hemos realizado una simplificación del ejemplo de 2 vehículos y 2 tareas incluido en la demostración de la API y lo hemos modelado con Pyomo. El código completo utilizado para ejecutar con CuOpt y pyomo está disponible al final de esta entrada de blog, en la sección Ejemplo ficticio ejecutado con CuOpt y Pyomo del apéndice. Aquí, trataremos solo los aspectos más relevantes del modelo de problemas de la LMD para los entusiastas de las operaciones de investigación.

Las simplificaciones realizadas en las restricciones del ejemplo son que ahora ambos vehículos tienen los indicadores skip_first_trips y skip_first_trips como False, las restricciones de capacidad/demanda se redujeron a una sola dimensión por vehículo y se excluyeron las variables relacionadas con los descansos.

En las siguientes secciones se asume que la variable pyomo_data tiene los parámetros problemáticos cargados en sus campos respectivos. Incluso con las simplificaciones mencionadas para el problema del ejemplo de carga útil, el modelo dio como resultado las siguientes definiciones.

Parámetros

Los nodos enumeran las ubicaciones posibles (0, 1 y 2), los vehículos son las 2 etiquetas de vehículos («veh-i») y task_locations son las 2 ubicaciones de tareas (1 y 2). La ubicación 0 es el depósito.

model.nodes = Set (initialize=pyomo_data ["nodes"])

model.vehicles = Set (initialize=pyomo_data ["vehicles"])

model.task_locations = Establecer (initialize=pyomo_data ["task_locations"])

def initialize_cost_matrix (modelo, v, i, j):

regresar pyomo_data ["matriz_coste"] [v] [i] [j]

model.cost = Parámetro (

modelo de vehículos,

modelo.nodos,

modelo.nodos,

initialize=initialize_cost_matrix

)

model.vehicle_max_cost = Parámetro (

modelo de vehículos,

inicializar=lambda modelo, v: pyomo_data ['vehicle_max_costs'] [list (model.vehicles) .index (v)]

)

def initialize_time_cost_matrix (modelo, v, i, j):

regresar pyomo_data ["matriz_tiempo_coste"] [v] [i] [j]

model.time_cost = Parámetro (

modelo de vehículos,

modelo.nodos,

modelo.nodos,

initialize=initialize_time_cost_matrix

)

model.vehicle_capacity = Parámetro (

modelo de vehículos,

inicializar=lambda modelo, v: pyomo_data ["capacidades"] [list (model.vehicles) .index (v)]

)

model.demand = Param (

model.task_locations,

inicializar=lambda modelo, i: pyomo_data ["demanda"] [list (model.task_locations) .index (i)]

)

model.vehicle_time_window_start = Parámetro (

modelo de vehículos,

inicializar=lambda modelo, v: pyomo_data ["vehicle_time_windows"] [list (model.vehicles) .index (v)] [0]

)

model.vehicle_time_window_end = Parámetro (

modelo de vehículos,

inicializar=lambda modelo, v: pyomo_data ["vehicle_time_windows"] [list (model.vehicles) .index (v)] [1]

)

model.vehicle_max_time = Parámetro (

modelo de vehículos,

inicializar=lambda modelo, v: pyomo_data ['vehicle_max_times'] [list (model.vehicles) .index (v)]

)

model.task_time_window_start = Parámetro (

modelo.nodos,

inicializar=lambda modelo, i: pyomo_data ['task_time_windows'] [list (model.task_locations) .index (i)] [0] si ¡Hola! = 0 más Ninguna

)

model.task_time_window_end = Parámetro (

modelo.nodos,

inicializar=lambda modelo, i: pyomo_data ['task_time_windows'] [list (model.task_locations) .index (i)] [1] si ¡Hola! = 0 más Ninguna

)

Variables de decisión

modelo.x = Var (

modelo de vehículos,

modelo.nodos,

modelo.nodos,

Dominio=binario

)

model.t = Var (

modelo de vehículos,

modelo.nodos,

Domain=Reales no negativos

)

Restricciones

#1. Cada tarea debe ser atendida una vez

def task_served_rule (modelo, i):

si ¡Hola! = 0:

regresar suma (model.x [v, j, i] por v en modelo. vehículos por j en modelo.nodes si ¡j! = i) == 1

regresar Restricción. Omitir

model.task_served = Restricción (model.nodes, rule=task_served_rule)

#2. Evita los círculos triviales (x [v, i, i] = 0 para todos los v, i)

def no_self_loops_rule (modelo, v, i):

regresar modelo.x [v, i, i] == 0

model.no_self_loops = Restricción (model.vehicles, model.nodes, rule=no_self_loops_rule)

#3. Cada vehículo debe salir y regresar al depósito

def leave_depot_leave_rule (modelo, v):

# Asegúrese de que el vehículo salga del depósito al menos una vez

regresar suma (model.x [v, 0, j] por j en modelo.nodes si ¡j! = 0) == 1

model.leave_depot_leave = Restricción (model.vehicles, rule=leave_depot_leave_rule)

def leave_depot_return_rule (modelo, v):

# Asegúrese de que el vehículo regrese al depósito después de visitar las tareas

regresar suma (model.x [v, i, 0] por i en modelo.nodes si ¡Hola! = 0) == 1

model.leave_depot_return = Restricción (model.vehicles, rule=leave_depot_return_rule)

Nº 4. Solo puede haber una transición de una ubicación a otra si la ubicación de salida se visitó anteriormente

def valid_flow_rule (modelo, v, i, j):

si ¡Hola! = j e i! = 0 y j! = 0:

regresar modelo.x [v, i, j] <= suma (modelo.x [v, k, i] por k en modelo.nodes si ¡k! = i)

regresar Restricción. Omitir

model.valid_flow = Restricción (model.vehicles, model.nodes, model.nodes, rule=valid_flow_rule)

Nº 5. Límites máximos de coste y tiempo por vehículo

def vehicle_max_cost_rule (modelo, v):

regresar suma (model.cost [v, i, j] * model.x [v, i, j] por i en modelo.nodes por j en model.nodes) <= model.vehicle_max_cost [v]

model.vehicle_max_cost_constraint = Restricción (model.vehicles, rule=vehicle_max_cost_rule)

def regla_max_time_rule del vehículo (modelo, v):

regresar suma (model.time_cost [v, i, j] * model.x [v, i, j] por i en modelo.nodes por j en modelo.nodes) <= modelo.vehicle_max_time [v]

model.vehicle_max_time_constraint = Restricción (model.vehicles, rule=vehicle_max_time_rule)

Nº 6. Restricción de capacidad: la demanda total de un vehículo no puede superar su capacidad

def regla_restricción_capacidad (modelo, v):

regresar suma (model.demanda [i] * suma (model.x [v, j, i] por j en modelo.nodes si ¡j! = i) por i en model.task_locations) <= model.vehicle_capacity [v]

model.capacity_constraint = Restricción (model.vehicles, rule=capacity_constraint_rule)

Nº 7. Asegúrese de que la hora de inicio de cada vehículo en el depósito esté dentro de su período de tiempo

def vehicle_time_window_lower_rule (modelo, v):

regresar model.vehicle_time_window_start [v] <= modelo.t [v, 0]

def vehícule_time_window_upper_rule (modelo, v):

regresar modelo.t [v, 0] <= modelo.vehicle_time_window_end [v]

## Agregue las restricciones para las ventanas de tiempo de inicio y finalización

model.vehicle_time_window_lower_constraint = Restricción (

model.vehicles, rule=vehicle_time_window_lower_rule

)

model.vehicle_time_window_upper_constraint = Restricción (

model.vehicles, rule=vehicle_time_window_upper_rule

)

Nº 8. Límite de tiempo para las tareas

# Restricción de límite inferior de la ventana de tiempo de la tarea

def task_time_window_lower_rule (modelo, v, i):

si ¡Hola! = 0: # Skip depot (nodo 0)

regresar model.task_time_window_start [i] <= modelo.t [v, i]

regresar Restricción. Omitir

# Restricción del límite superior de la ventana de tiempo de la tarea

def task_time_window_upper_rule (modelo, v, i):

si ¡Hola! = 0: # Skip depot (nodo 0)

regresar model.t [v, i] <= model.task_time_window_end [i]

regresar Restricción. Omitir

model.task_time_window_lower_constraint = Restricción (

model.vehicles, model.nodes, rule=task_time_window_lower_rule

)

model.task_time_window_upper_constraint = Restricción (

model.vehicles, model.nodes, rule=task_time_window_upper_rule

)

Función objetiva

# Función objetivo: minimizar el costo total de las rutas

def objective_rule (modelo):

regresar suma (

modelo.costo [v, i, j] * modelo.x [v, i, j]

por v en modelo. vehículos

por i en modelo.nodes

por j en modelo.nodes

)

model.objective = Objetivo (regla = regla objetiva, sentido = minimizar)

Resolviendo el modelo

solucionador = SolverFactory ('glpk')

resultado = solver.solve (modelo, tee=Cierto)

Tanto la solución con CuOpt como la de Pyomo generaron la misma solución de enrutamiento de vehículos. Dado que se trata de un ejemplo ficticio en el que intervienen 3 ubicaciones, 2 vehículos y 2 tareas, es sencillo visualizar como solución factible una ruta en la que cada vehículo realice la tarea de menor coste y, a continuación, regrese al depósito. Además, en un conjunto de datos de dimensiones tan bajas, el mayor rendimiento de CUOPT con respecto al de Pyomo no está representado de manera justa.

Este ejemplo sigue siendo muy útil para comprender mejor el uso de CuOpt, así como para obtener información sobre lo que ocurre entre bastidores y cómo (¿divertido? ¿doloroso?) sería modelar el problema del VRP desde cero.

Análisis de tiempo y costo de CuOpt en un conjunto de datos grande

Como la API CuOpt proporciona una solución en relación con el parámetro de límite de tiempo, ejecutará la optimización durante ese tiempo y proporcionará la solución óptima que se encontró. Por lo tanto, diferentes plazos podrían corresponder a diferentes soluciones. Los valores de la función de costo a lo largo del proceso iterativo no se proporcionan en la respuesta.

Por lo tanto, para analizar la estabilidad del costo total a lo largo de las iteraciones, ejecutamos un escenario simple de solicitudes consecutivas con los mismos parámetros de LMD, estableciendo el límite de tiempo en 5 segundos al principio, luego en intervalos de 15 segundos, 30 segundos, 60 segundos y más de 30 segundos hasta 6 minutos.

Para aumentar las apuestas, el conjunto de datos utilizado para modelar el problema del LMD para este análisis tiene una dimensionalidad mucho mayor que el problema ficticio: tiene 100 ubicaciones, 97 tareas y hasta 10 vehículos con diferentes capacidades.

El costo resultante de estas ejecuciones consecutivas se muestra en la siguiente gráfica:

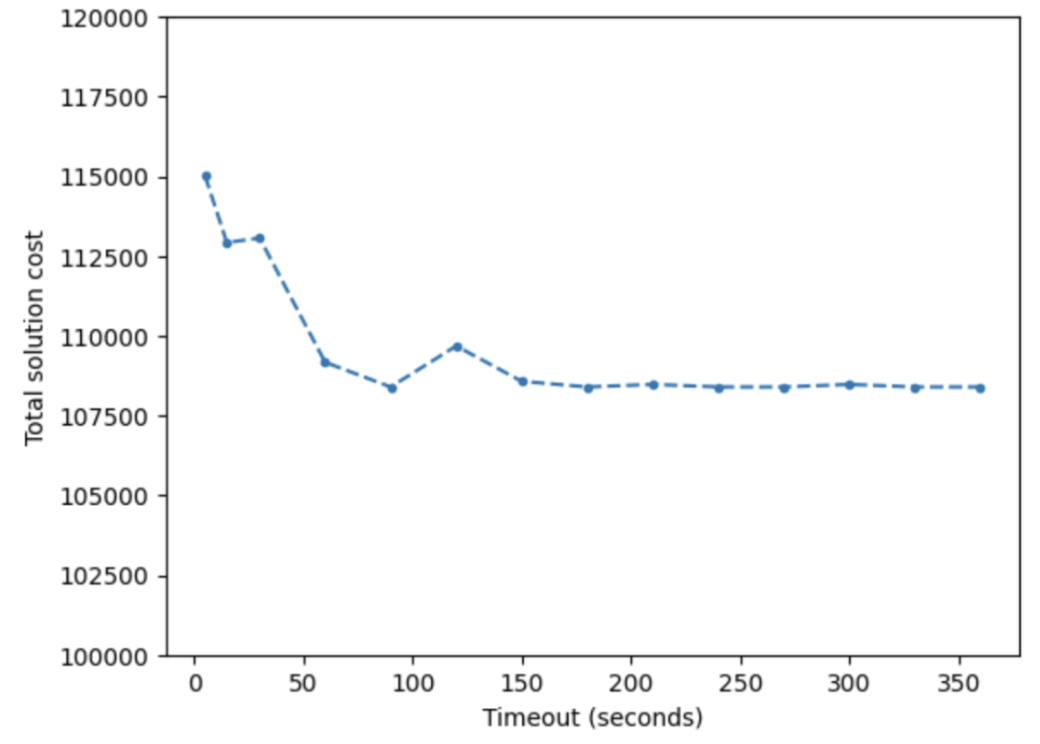
Las tiradas iniciales pueden encontrar una solución factible con un coste total de 115 000, mientras que el valor estable aparece en las tiradas con un tiempo de espera de 150 segundos o más, con un coste aproximado de 108 000. En este ejemplo, el costo de la solución instantánea es solo un 6,5% más alto que el costo estable encontrado después de una ejecución de 2 minutos.

La compensación entre la optimización instantánea y un retraso de 2 minutos con una variación de costos del 6,5% depende realmente del impacto que dichos costos representen para la industria en cuestión. Sin embargo, no cabe duda de que lograr un margen tan bajo en una respuesta casi en tiempo real durante un proceso iterativo para un problema de optimización con una dimensionalidad tan alta es ciertamente impresionante, en términos de optimización computarizada.

Bonificación: ¿Y qué pasa con Pyomo?

En un intento de comparar el rendimiento de CuOpt con el de pyomo, modelamos el problema de LMD para este gran conjunto de datos siguiendo la misma lógica que utilizamos al implementar el ejemplo ficticio.

Dejando de lado los costes irrecuperables de modelar teóricamente un problema de tan alta dimensionalidad con pyomo, se necesitaron al menos 30 segundos en una computadora con CPU de 8 GB para encontrar una solución factible como punto de partida. Incluso cuando se ejecutaba con scip solver (superior al glpk estándar), ni siquiera después de 3 horas de ejecución de la optimización, el algoritmo pudo encontrar una solución cercana a distancia desde el punto de vista económico.

Esto nos permitió concluir que un problema de dimensiones tan altas es pedir demasiado a un PC, mientras que CuOpt puede encontrar una solución razonable al instante y una aún más precisa en 5 minutos.

Conclusión

Cuando se trata de un problema de enrutamiento de vehículos (VRP), CuOpt es un microservicio altamente eficiente y fácil de usar. Para dichos problemas, admite millones de variables y restricciones, lo que puede suponer una enorme ventaja frente a la posibilidad de trabajar localmente (lo que resulta poco realista desde el punto de vista computacional) o de modelar el problema desde cero en un marco diferente. Al usar CuOpt, un desarrollador no necesita ser un especialista en investigación de operaciones para modelar un problema de enrutamiento con varias restricciones y puede ahorrarse el tiempo de modelar un problema matemático, que suele ser la parte más difícil de la resolución de un problema de optimización.

¿Cuándo usar CuOpt?

Recomendamos adoptar CuOpt en escenarios en los que se aplique el modelo de optimización de VRP, con altos requisitos de recálculo frecuente y necesidades de optimización en tiempo real.

Dicho esto, el VRP es solo una fracción de la familia de problemas de optimización MILP. En cuanto al resto de los problemas personalizados de investigación operativa que puedan surgir, seguiríamos recurriendo a marcos más flexibles en cuanto a modelos, como Pyomo. Sin embargo, es posible que necesitemos reevaluar nuestras opciones si estuvieran disponibles las funciones de programación lineal y programación lineal de enteros mixtos...

¿Quién podría beneficiarse de esto?

Algunos ejemplos son las empresas de logística que se encargan de las entregas del productor al consumidor, las agencias que brindan servicios de mensajería desde entregas de última milla hasta el envío de contenedores, las aplicaciones de entrega en restaurantes, cualquier empresa que aproveche las ventas puerta a puerta, entre otras.

Kawasaki Heavy Industries y SyncTwin se encuentran entre las empresas que ya se han beneficiado del uso de CuOpt. Según Kawasaki, se estima que un sistema de este tipo impulsado por la inteligencia artificial puede ahorrar 218 millones de dólares al año a siete empresas al automatizar sus inspecciones en vías.

Problemas con los datos

Por último, al igual que en cualquier otro microservicio de consumo de API, se deben tener en cuenta las políticas y los requisitos de datos confidenciales. Es difícil imaginar que un problema de VRP pueda implicar información confidencial, especialmente porque la optimización es con frecuencia una línea de trabajo que se explora en situaciones en las que no hay suficientes datos disponibles para una solución de aprendizaje automático. Sin embargo, para seguir siendo proveedores éticos, las políticas de tratamiento de datos de los clientes deben cumplir en todo momento con la política de tratamiento de los datos procesados de los proveedores.

Si dicho escenario fuera el caso, hay técnicas de codificación que podrían usarse. Por obvio que parezca, como regla general, evite utilizar correos electrónicos personales para etiquetar como identificadores de vehículos en la carga útil de datos de CuOpt.

¿Qué es lo siguiente?

CuOpt nos ha llevado hasta aquí en lo que respecta a los problemas de enrutamiento de vehículos. Nos entusiasma saber lo que CuOpt tiene para ofrecer con sus próximas funciones de programación lineal y programación lineal de enteros mixtos.

Es probable que se estén desarrollando más líneas de trabajo de optimización. Si NVIDIA continúa por este camino, podrían convertirse en actores clave en el negocio de la «optimización como servicio».

Referencias

• Introducción a la programación lineal de números enteros mixtos (MILP)
• Vídeo de demostración de CuOpt
• Demostración de la API CuOpt
• Guía de usuario de NVIDIA CuOpt
• Enviar a solver Referencia de punto final POST
• Recursos de CUOpt repositorio: contiene una colección de recursos que demuestran el uso de NVIDIA CuOpt a través de las API de servicio. Fuente del gran conjunto de datos (100 ubicaciones, 97 tareas, 10 vehículos) utilizado en el análisis de tiempos y costes.
• All Aboard: NVIDIA consigue 23 récords mundiales en optimización de rutas: Entrada de blog del sitio web de NVIDIA

Anexo

Payload de solicitud de ejemplo de CUOpt

Esta es la carga útil que se explica en la sección «¿Cómo traducir LMD a la carga útil de CuOpt?» sección. Es la misma que se proporciona en la Demostración de la API CuOpts sitio en la fecha actual.

carga útil = {

«action»: «cuOPT_OptimizedRouting», # o cuopt_LP si estaba disponible

«datos»: {

«cost_waypoint_graph_data»: Ninguna,

«travel_time_waypoint_graph_data»: Ninguna,

«datos_matrix_costales»: {

«datos»: {

«1": [0,1,1],

[1, 0,1],

[1,1, 0],

«2»: [0, 1,1],

[1,0,1],

[1,2, 0]

}

},

«datos_matrix_tiempo_viaje»: {

«datos»: {

«1": [0,1,1],

[1, 0, 1],

[1,1,0],

«2": [0,1, 1],

[1,0,1],

[1,2, 0]

}

},

«datos_de la flota»: {

«localizaciones del vehículo»: [[0,0],

[0, 0],

«vehicle_ids»: ["veh-1", «veh-2"],

«capacidades»: [[2,2], [4,1]],

«vehicle_time_windows»: [[0, 10],

[0, 10],

«vehicle_break_time_windows»: [

[1, 2],

[2,3]

],

«vehicle_break_durations»: [[1, 1]],

«vehicle_break_locations»: [0, 1],

«tipos de vehículos»: [1, 2],

«vehicle_order_match»: [

{

«order_ids»: [0],

«id_vehículo»: 0

},

{

«order_ids»: [1],

«id_vehículo»: 1

}

],

«saltarse los primeros viajes»: [ Cierto, Falso ],

«drop_return_trips»: [ Cierto, Falso],

«vehículos mínimos»: 2,

«vehicle_max_costs»: [7, 10],

«vehicle_max_times»: [7, 10]

},

«datos_tareas»: {

«task_locations»: [1, 2],

«task_ids»: [«Tarea-A», «Tarea-B"],

«demanda»: [[1, 1],

[3, 1],

«task_time_windows»: [[0, 5],

[3,9],

«tiempos de servicio»: [0, 0],

«order_vehicle_match»: [

{

«order_id»: 0,

«identificaciones del vehículo»: [0]

},

{

«order_id»: 1,

«identificaciones del vehículo»: [1]

}

]

},

«solver_config»: {

«límite de tiempo»: 1,

«objetivos»: {

«costo»: 1,

«tiempo_viaje»: 0,

«variance_route_size»: 0,

«variance_route_service_time»: 0,

«premio»: 0

},

«modo_detallado»: Falso,

«registro de errores»: Cierto

}

},

«versión_cliente»: «»

}

‍