.png)
Introducción a la programación lineal de números enteros mixtos (MILP)
Introducción
Hoy en día, cuando pensamos en resolver problemas complejos con ordenadores, inmediatamente pensamos en big data y aprendizaje automático. El desarrollo de una solución de aprendizaje automático suele requerir una cantidad intensiva de datos, que utilizamos para extraer los patrones y las reglas que subyacen al comportamiento de nuestros sistemas. Pero, ¿qué sucede cuando estos datos no son suficientes o, lo que es peor, no hay datos disponibles en absoluto? Si conocemos esas reglas de antemano, la programación lineal de enteros mixtos (MILP) podría ser la elección correcta. La MILP es una subárea del área más amplia llamada optimización convexa, y básicamente implica dos pasos: el modelado y la optimización. Modelar un problema es el arte de expresar un escenario del mundo real como un conjunto de ecuaciones y restricciones objetivas. El proceso de optimización en sí mismo está relacionado con la búsqueda de la mejor solución posible para el objetivo teniendo en cuenta las restricciones. A través del MILP se pueden expresar y resolver muchos de los problemas habituales de la industria. Maximizar el flujo de caja en la industria financiera, encontrar la ruta óptima para un problema de transporte y encontrar una asignación efectiva de recursos para una aplicación de fabricación, solo por nombrar algunos. En este blog, nos sumergimos en las aplicaciones prácticas de optimización. Empezamos proponiendo un problema de asignación de productos y modelándolo utilizando un marco MILP. Este ejemplo también nos permitirá explorar algunos detalles fundamentales de las técnicas del MILP y, finalmente, implementaremos el problema modelado en Python usando la biblioteca Pyomo.
Programación lineal de números enteros mixtos versus aprendizaje automático
Aunque podemos usar el aprendizaje automático (ML) y la programación lineal de enteros mixtos (MILP) para resolver algunos de los mismos problemas (a veces de forma complementaria), el enfoque es bastante diferente. El proceso típico de aprendizaje automático comienza con la recopilación y limpieza de enormes cantidades de datos, para luego entrenar un modelo que aprenda la distribución subyacente de los datos para explicar el mundo real. En el caso del MILP, necesitamos confiar en los expertos para diseñar un conjunto de reglas que expliquen el mundo real a través de las matemáticas. Al principio, parece que el aprendizaje automático es un enfoque superior, ya que puede aprender directamente de los datos. Sin embargo, cuando no tenemos suficientes datos, tenemos reglas comerciales claramente definidas o queremos poder influir y modificar el comportamiento de nuestro sistema de forma transparente, MILP brilla. Si comparamos el campo de la optimización con los avances más vanguardistas de la inteligencia artificial, se podría argumentar que la optimización parece algo anticuada. Desde finales de los 70, los matemáticos han estado desarrollando la teoría de la optimización, especialmente la teoría de la programación lineal de números enteros mixtos. Si bien estos métodos existen desde hace bastante tiempo, los avances recientes en los algoritmos de optimización y la potencia informática bruta han permitido resolver enormes problemas de optimización multivariante con miles (o quizás millones) de parámetros en cuestión de minutos.
¿Qué podemos resolver con MILP?
Hay una gran variedad de problemas que pueden abordarse con MILP, veamos ejemplos rápidos de algunos de ellos [1]: 💵 Optimización del flujo de caja se puede lograr eligiendo en qué instrumentos financieros invertir y durante cuánto tiempo de acuerdo con nuestro capital disponible para maximizar la rentabilidad o minimizar el riesgo. 🛒 Asignación de productos es el proceso de asignar una variedad de productos a diferentes estantes para maximizar los ingresos. En el ejemplo, asignaremos libros de diferentes tamaños y precios a las estanterías disponibles, teniendo en cuenta que algunas estanterías tienen más visibilidad que otras. 🏭 Asignación de recursos es el proceso de asignar estratégicamente los recursos disponibles a diferentes tareas. En la fabricación, resolveríamos cómo asignar los trabajadores y los materiales disponibles a nuestras diferentes líneas de producción para maximizar nuestras ganancias totales o minimizar el costo total. 🕰️ Programación es similar a la asignación de recursos, pero teniendo en cuenta la temporalidad. Dado un conjunto de recursos, los asignamos a las tareas en un tiempo determinado. Por ejemplo, si necesitamos asignar a los trabajadores por turnos, teniendo en cuenta su disponibilidad y habilidades, podemos calcular el mejor cronograma posible. 🛵 Planificación de rutas es lo que hacen todas las empresas de entrega de alimentos. Dado un origen y múltiples destinos, elige la mejor ruta según algunos criterios. Minimizar el consumo de combustible, minimizar los tiempos de entrega promedio o maximizar la cantidad de artículos entregados en un tiempo determinado. ✈️ Redes de transporte son una de las muchas aplicaciones de los flujos de red. Una empresa de transporte que tiene que entregar mercancías desde una ciudad de origen a una ciudad de destino, sin embargo, no hay vuelos directos entre esas ciudades. Hay ciudades intermedias que pueden conectar indirectamente el origen y el destino, pero los vuelos tienen diferentes límites en cuanto a la cantidad de mercancías que pueden transportar. Al modelar este problema, podemos maximizar la cantidad de bienes que llegan a destino desde su origen.
Conceptos básicos de MILP
En esta sección, nos centraremos en los fundamentos de la programación lineal de enteros mixtos. No vamos a entrar en muchos detalles matemáticos sobre la formulación, pero proporcionaremos un contexto general antes de pasar directamente a una aplicación. También definiremos algo de la jerga del MILP.
Planteamiento del problema
Imagina que tenemos un función objetiva llamada Y necesitamos optimizar, por ejemplo, el número total de productos en una asignación de productos. Tenemos un conjunto de parámetros que contienen información fija previa sobre el problema, como los precios de los productos, los tamaños, las dimensiones de los estantes y otros valores fijos. Necesitamos algo que podamos modificar para lograr lo óptimo de nuestra función objetivo. Para ello, tenemos variables de decisión, que representan cualquier variable libre que deba determinarse al resolver el problema y se indican con la letra x. Por ejemplo, las posiciones de cada uno de nuestros productos. Los valores posibles de las variables de decisión deben verificar un conjunto de condiciones lineales externas denominadas restricciones. Si tenemos M restricciones que dependen linealmente de las variables de decisión, podemos formular el problema de la siguiente manera [2]:
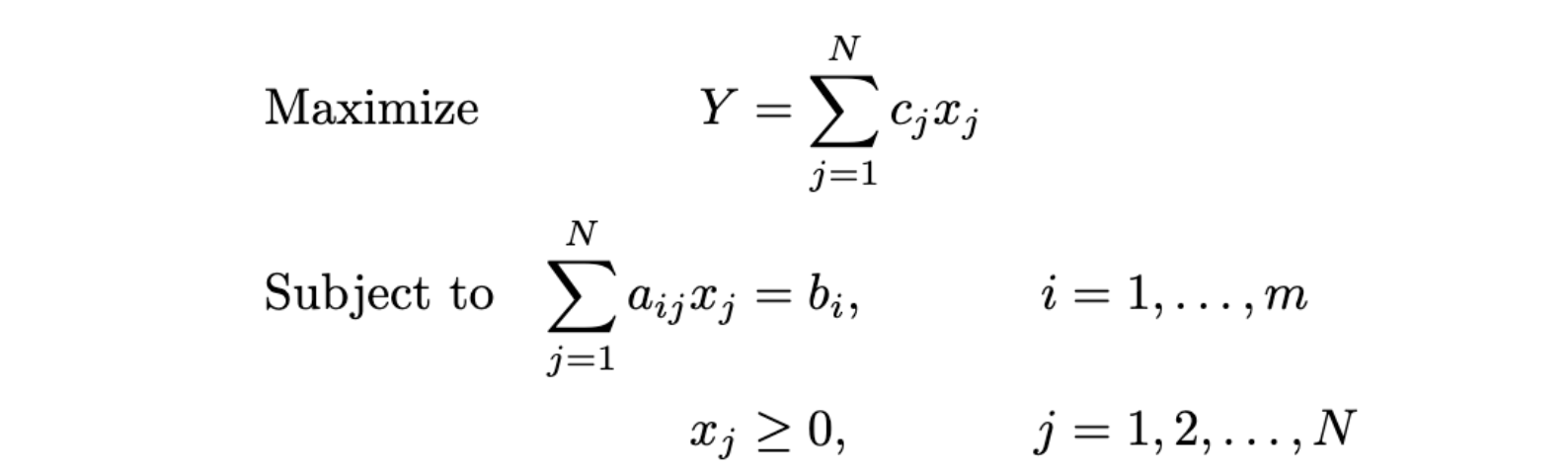
Resolver este problema implica encontrar un conjunto de valores x que maximiza (o minimiza) el resultado Y. Las limitaciones pueden ser igualdades o desigualdades y podríamos tener un número arbitrario de ellas. Como se mencionó anteriormente, este marco puede modelar una amplia variedad de problemas en diferentes industrias. El éxito en esta área depende de la capacidad de traducir escenarios del mundo real en conjuntos de ecuaciones. A continuación, aplicamos este marco a un problema de asignación de productos.
Programación no lineal
Esta formulación del MILP se puede extender a otras áreas dentro de la investigación de operaciones. Si algunas de las restricciones, o incluso la función objetivo, incluyen alguna falta de linealidad, aún es posible resolver el problema de optimización. Esto requiere la aplicación de un conjunto diferente de técnicas, conocidas como programación no lineal de enteros mixtos (MINLP). Sin embargo, también se pueden utilizar las técnicas MILP tradicionales para aproximar variables no lineales linealizándolas en el intervalo de interés. Esto conduciría lógicamente a soluciones aproximadas, pero en la mayoría de los casos, estas soluciones son lo suficientemente buenas para los problemas de aplicación.
La optimización en la práctica: asignación de productos
Una librería en línea quiere abrir su primera tienda física, y uno de los desafíos a los que se enfrenta es cómo colocar los libros en las estanterías para maximizar los ingresos. Para solucionarlo, decidieron ponerse en contacto con nosotros, expertos en optimización, para que les ayudáramos a solucionar su problema. Resumimos sus requisitos en la siguiente declaración: Tenemos que colocar tantos libros como podamos en las estanterías, colocar los libros más populares en las estanterías más visibles y mantener a los mismos autores juntos. Como se mencionó en la sección anterior, necesitamos identificar los parámetros, las variables, las restricciones y la función objetivo, de modo que podamos encontrar la solución óptima. Es una práctica común definir verbalmente estos componentes de la solución para luego formularlos matemáticamente. Parámetros: Para cada libro, necesitamos una medida de su popularidad, precio, autor y dimensiones. A su vez, para cada estante de las estanterías, necesitamos saber las dimensiones y la visibilidad o exposición que proporcionan a los libros. Variables: Para cada libro, necesitamos saber en qué estante y en qué lugar de ese estante debe estar ubicado. Restricciones: Solo debemos incluir una copia de cada libro y deben caber en la estantería por altura. La longitud total de los libros seleccionados en una estantería debe coincidir con el ancho de la estantería. Además, los libros del mismo autor deben estar en la misma estantería. Función objetiva: Los ingresos de cada libro se definen por el precio del libro, su popularidad y la visibilidad que proporciona su ubicación. Nuestro objetivo es maximizar los ingresos totales, como la suma de los ingresos de todos los libros asignados.
Conjuntos
En primer lugar, definimos el conjunto de índices que utilizaremos para definir nuestro problema. Como tendremos muchas variables y parámetros que se repiten para cada libro, librería y autor, los índices facilitan mucho la notación.
- El conjunto B representa el conjunto de libros considerados para el problema. Cada libro individual se referirá con el subíndice b.
- El conjunto C representa el conjunto de estanterías consideradas para el problema. Cada estantería individual se referirá con el subíndice c.
- El conjunto UN representa el conjunto de autores considerados para el problema. Cada autor individual será referido con el subíndice un.
- El conjunto S representa el conjunto de estantes considerado para el problema. Cada estante individual se referirá con el subíndice s.
Parámetros
Luego definimos los parámetros del problema, que representan la información y las configuraciones anteriores, es decir, valores que no podemos modificar en nuestro proceso de optimización:
Libros
- Definimos el parámetro b_popb como la popularidad del libro b.
- Definimos el parámetro b_widthp como el ancho en mm para el libro b.
- Definimos el parámetro b_heightb como la altura en mm del libro b.
- Definimos el parámetro b_preciob como precio en USD por libro b.
- Definimos el parámetro booleano es_autora, b lo cual es cierto si el libro b fue escrito por el autor un y falso si no.
estanterías
- Definimos el parámetro s_widthc, s como el ancho en mm para estante s de bookcase c.
- Definimos el parámetro s_heightc, s como la altura en mm del estante s de bookcase c.
- Definimos los parámetros s_visibilidadc, s como la visibilidad que gana un libro al colocarlo en una estantería b de bookcase c.
Variables de decisión
A continuación, debemos identificar las variables de decisión cuyos valores se deben encontrar en el proceso de optimización. Estas variables representan todos los valores que podemos modificar como profesionales:
- Definimos la variable booleana Es_Book_Atb, c, s que representa si libro b está en el estante s de estantería c.
- Definimos la variable booleana Es_Autor_Ena, c, s que representa si el autor un está en el estante s de estantería c.
Restricciones
Ahora, una vez definidas las variables de decisión, necesitamos definir matemáticamente todas las restricciones del problema. Nuestra primera restricción está relacionada con la limitación del número de veces que podemos asignar un libro.
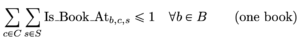
De esta manera, nos aseguramos de que cada libro se asigne como máximo una vez, lo que también permite que la modelo omita libros si no caben. Hay dos restricciones que tienen que ver con el tamaño de las estanterías:


Para limitar el número de estanterías en las que aparece un autor, necesitamos rellenar la variable accesoria Es_Autor_Ena, c, s. Esto se puede hacer mediante la combinación de dos restricciones.
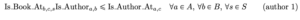
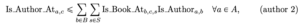
Luego debemos asegurarnos de que cada autor aparezca como máximo en una estantería:

Función objetiva
Por último, necesitamos definir la función objetivo que estamos intentando maximizar. En este caso, los ingresos esperados de una venta específica de libros:

Después de formular el problema, resolverlo pasa a ser cuestión de utilizar solucionadores de programación lineal estándar. Hay muchos solucionadores de código abierto como GLPK de GNU, GLOP, y CP-SAT desarrollado por Google y muchos más.
Optimización de la asignación de productos con Pyomo
Ahora que el problema está completamente definido, es el momento de implementarlo usando Piomón [3], una biblioteca de código abierto basada en Python que admite un conjunto diverso de capacidades de optimización para resolver modelos de optimización. Si bien la utilizaremos para resolver un problema lineal, también tiene capacidades no lineales para resolver problemas más complejos. ¡Ahora es el momento de empezar a llenar nuestras estanterías!

Conjunto de datos
Para resolver nuestro problema, necesitamos datos de libros. Trabajaremos con un conjunto de datos de libros de fantasía (inspirados en esto). conjunto de datos). Incluye características del libro, como las dimensiones, la información del autor y las ventas promedio. La popularidad de un libro se puede deducir por el promedio de ventas. Luego necesitamos medir nuestras estanterías imaginarias para definir el espacio disponible para los libros. Para este ejemplo, trabajaremos con 3 estanterías, de 5 estantes cada una, con 1 metro de ancho y lo suficientemente altas como para almacenar las más altas. Cada estantería también tiene su propio factor de visibilidad, que multiplica las ventas de libros a medida que los colocamos en esta estantería. Echemos un vistazo a los datos con los que alimentaremos el modelo.

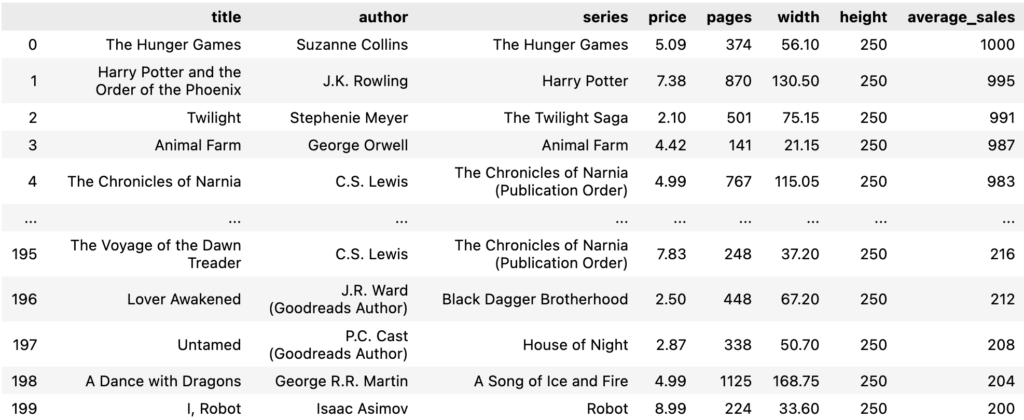
modelo
Parámetros
Una característica interesante de Pyomo es que nos permite definir variables y parámetros del modelo de forma funcional. Usando la notación definida en la sección anterior, tenemos nuestros conjuntos: # Defina los conjuntos Model.B = PyO.set (initialize=book_ids, doc="Books») model.S = PyO.set (initialize=shelf_ids, doc="Shelfs») model.C = PyO.set (initialize=bookcase_ids, doc="Bookcases») model.A = PyO.set (initialize=author_ids, doc="Authors») Y nuestros parámetros: # Defina los parámetros model.b_width = PyO.param (model.B, initialize=lambda model, b: book_widths [b], within=pyo.NonNegativeReals, doc="Width of book b»,) model.b_height = pyo.param (model.B, initialize==modelo lambda, b: book_heights [b], within=pyo.NonNegativeReals, doc="Altura del libro b»,) model.b_pop = pyo.Param (model.B, initialize=modelo lambda, b: book_average_sales [b], within=pyo.NonNegativeReals, doc="Ventas promedio del libro b»,) model.b_price = pyo.Param (model.B, initialize=lambda model, b: book_prices [b], within=pyo.NonNegativeReals, doc="Precio del libro b»,) model.is_author = pyo.param (model.B, model.a, initialize=lambda model, b, a: 1 if author_per_book [b] == a else 0, within=pyo.Binary, doc="es autor del libro «b»,) model.s_height = pyo.param (model.s, model.c, initialize=lambda model, s, c: shelf_heights [c, s], within=pyo.NonNegativeReals, doc="Altura de los estantes en la estantería c»,) model.s_width = pyo.param (model.s, model.c, initialize=lambda model, s, c: shelf_widths [c, s], within=pyo.NonNegativeReals, doc="Width of shelf s in bookcase c»,) model.s_visibility_factor = pyo.Param (Model.es, model.C, initialize=lambda model, s, c: shelf_visibility_factor [s], doc="Factor de visibilidad del estante s in bookcase c»,) De esta manera, le decimos a Pyomo que los anchos y las alturas son parámetros con componentes B y que los parámetros del estante tienen S veces C componentes, uno para cada estante de cada estantería. Esta formulación es bastante útil ya que nos permite modificar la dimensión de entrada sin cambiar este fragmento de código.
Variables de decisión
Ahora, definimos las variables de decisión y obligamos a nuestras variables de decisión a ser binarias. # Definimos las variables model.is_book_at = pyo.var (model.B, model.s, model.c, domain=PYO.Binary) model.is_author_at = pyo.var (model.A, model.c, domain=pyo.Binary)
Restricciones
A continuación, agregamos todas las restricciones al modelo. En Pyomo, se pueden definir las restricciones usando funciones regulares de Python. Estas funciones deben devolver un valor booleano basado en una condición de los parámetros y variables. Primero definimos todas las funciones: def __width_rule (model, s, c): return (sum (model.is_book_at [b, s, c] * model.b_width [b] para b en model.B) <= model.s_width [s, c]) def __height_rule (model, s, b, c): return (model.is_book_at [b, s, c] * model.b_height [b] <= model.s_height [s, c]) def __max_books_rule (model, b): suma de retorno (model.is_book_at [b, s, c] para s en model.C) <= 1 def __author_in_bookshelve_rule_1 (model, b, a, s, c): return (model.is_author_AT [a, c] >= model.is_book_at [b, s, c] * model.is_author [b, a]) def __author_in_bookshelve_rule_2 (modelo, a, c): return model.is_author_AT [a, c] <= sum (model.is_book_at [b, s, c] * model.is_author [b, a] para b en modelo.B para s en modelo.s) def __max_bookshelves_author_rule (model, a): return sum (model.is_author_AT [a, c] para c en modelo.is_author_AT [a, c] para c en modelo.<= 1 Y, a continuación, defina las restricciones: # Defina las restricciones model.width_constraint = PyO.constraint (Model.es, model.C, rule=width_rule, doc = «Todos los libros juntos de una estantería deben tener un ancho inferior al de la estantería») model.height_constraint = PyO.constraint (model.s, model.B, model.C, rule=height_rule, doc = «Los libros deben ser menos altos que la altura de los estantes» ) model.max_books_constraint = pyo.constraint (model.B, rule=max_books_rule, doc = «Cada libro debe estar en una sola estantería») model.author_in_bookshelve_constraint_1 = pyo.constraint (model.B, model.A, model.s, model.C, rule=author_in_bookshelve_rule_1, doc = «Rellenar si el autor está en la estantería») model.author_in_bookshelve_constraint_2 = pyo.constraint (model.A, model.C, rule=author_in_bookshelve_rule_2, doc = «Rellenar si el autor está en la estantería») model.max_bookshelves_author_constraint = pyo.Constraint (model.A, rule.A, ruleint =max_bookshelves_author_rule, doc = «Cada autor debe estar en solo una estantería»)
Función objetiva
El ingrediente final de nuestro modelo es la función objetiva. # Función objetiva def objective_function (model): total_books_earnings = sum (model.is_book_at [b, s, c] * model.b_price [b] * model.b_pop [b] * model.s_visibility_factor [s, c] para b en model.S para c en model.C) devuelve total_books_earnings model.cost = pyo.Objective (rule=objective_function, sense=pyo.maximize)
Resolviendo el modelo
Ahora por fin podemos resolver el modelo: # Select solver and solve solver = pyO.SolverFactory ('glpk') solution = solver.solve (model) Veamos cómo nos fue al modelar el problema. La siguiente imagen muestra cómo se ubicaban los libros en las estanterías. En naranja hemos resaltado los libros de J.K. Rowling, para mostrar que los libros del mismo autor están en la misma estantería.

Podemos ver que los libros caben bien en las estanterías, con poco o ningún espacio de sobra. Además, los libros delgados con un ancho y un precio más altos se encuentran en los estantes centrales, las partes más visibles de la estantería, mientras que los libros más gruesos y menos costosos se encuentran en los estantes inferiores. En la siguiente tabla se resumen algunas estadísticas sobre los resultados.
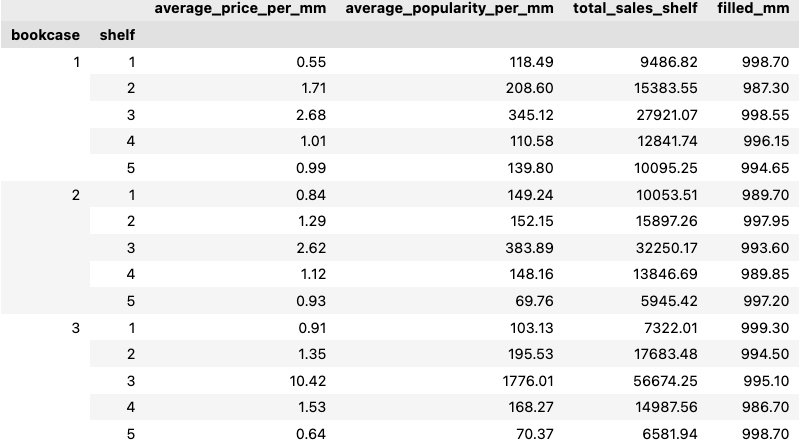
¿Qué pasaría si tuviéramos menos libros? Volvamos a ejecutar el modelo, pero eliminemos algunos de los libros menos populares de la lista de entrada.

Como era de esperar, la modelo opta por dejar espacios vacíos en una de las estanterías menos visibles. Colocar un libro allí en lugar de en una estantería con mayor visibilidad iría en contra del objetivo del modelo.
¿Podemos obtener siempre una solución óptima?
Al analizar las formulaciones de LP o MILP, vemos que las restricciones imponen algunas restricciones a los posibles valores de las variables de decisión. Hay combinaciones de valores que no cumplen con las restricciones y, por lo tanto, no son los candidatos óptimos. Formalmente, se puede evaluar la viabilidad del problema de optimización del MILP con las condiciones de Karush—Kuhn—Tucker (KKT). En aras de la simplicidad, no vamos a entrar en eso en este post. El conjunto de todas las combinaciones de variables de decisión que satisfacen todas las restricciones se denomina región factible, y resolver un problema de programación lineal implica encontrar el valor máximo (o mínimo) de una función objetivo dentro de esta región factible.
Soluciones factibles y limitadas
Para visualizar esta región factible, imagine que tenemos dos variables de decisión no negativas x1 y x2, y un conjunto de restricciones. Podríamos representar el problema en una gráfica bidimensional de la siguiente manera: [caption id="attachment_3102" align="aligncenter» width="350"]
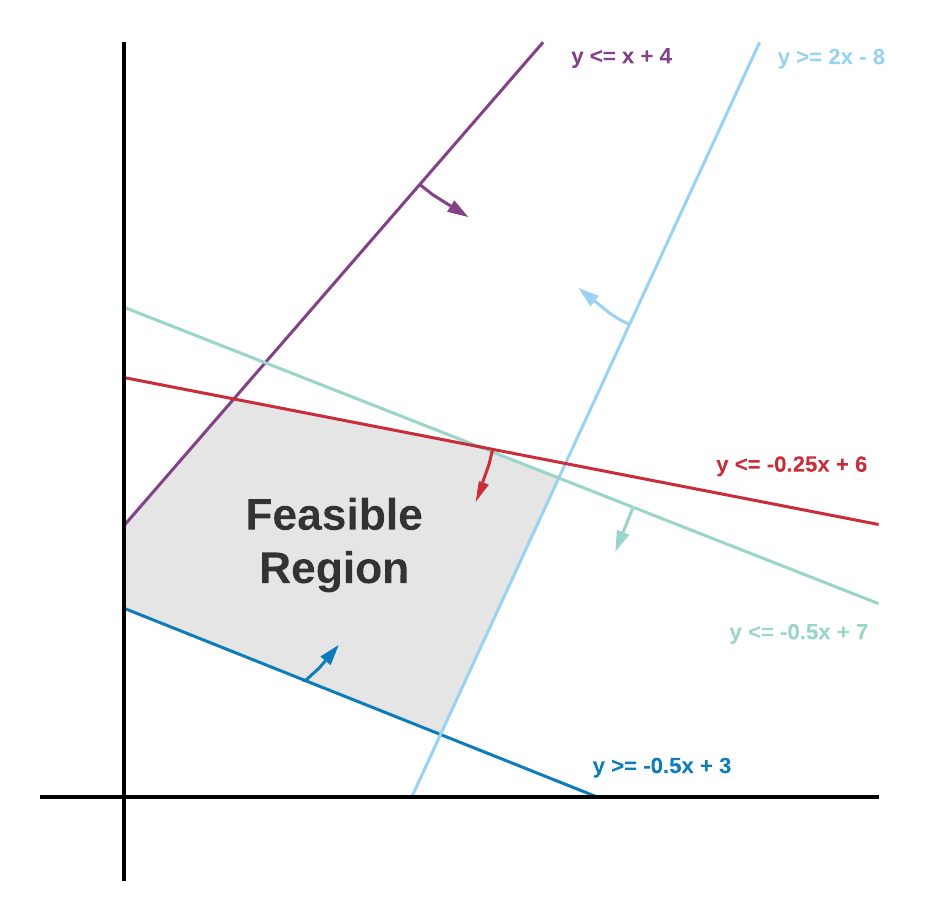
Delimitación de una región factible [4][/caption] La región factible en este caso es la región sombreada en gris, que representa todas las combinaciones posibles de x1 y x2 que satisfacen todas las restricciones al mismo tiempo. Los valores óptimos para la función objetivo estarán en uno de los vértices o bordes de la región factible. Por lo tanto, la esencia de la resolución de un problema de programación lineal es buscar los valores objetivos en estos puntos.
Soluciones inviables o ilimitadas
Nuestro problema podría implicar una solución factible y limitada, como en la imagen de arriba, pero esta región también podría ser inviable o ilimitada. Las regiones inviables aparecen cuando no hay una combinación de variables que pueda satisfacer todas las restricciones al mismo tiempo. Las regiones ilimitadas aparecen cuando el área factible es infinitamente grande. La siguiente imagen muestra la diferencia entre estos escenarios: [caption id="attachment_3093" align="aligncenter» width="788"]
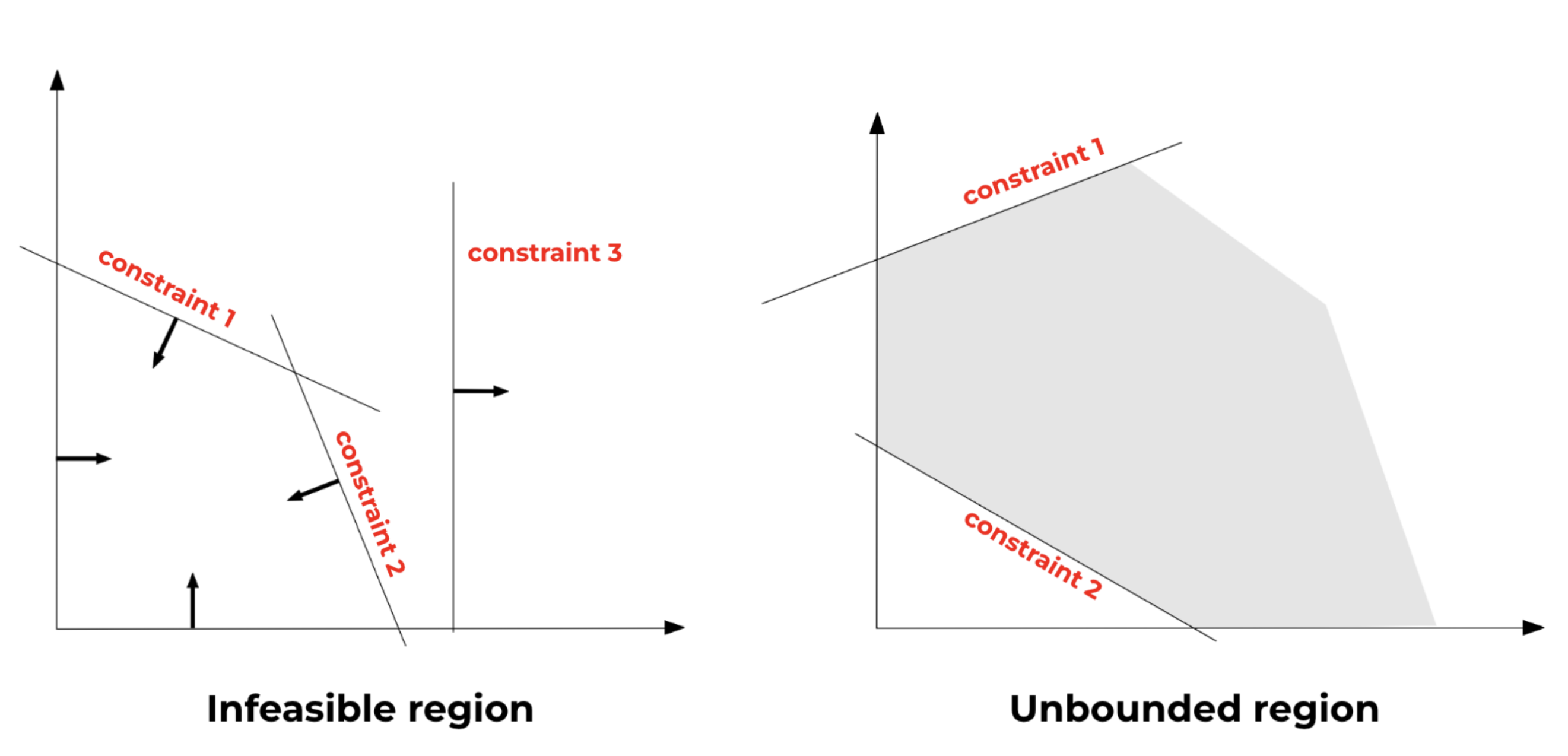
Imagen adaptada del manual de modelado de optimización de AIMMS [5][/caption] Dependiendo de forma de la región factible, el problema puede tener una solución o no, y podemos clasificar la solución del problema en tres escenarios diferentes:
- Solución óptima: en este caso, el problema está bien definido y es posible encontrar un valor óptimo de la función objetivo dentro de la región factible.
- Solución ilimitada: siempre que la función de maximizar (minimizar) pueda crecer (disminuir) infinitamente dentro de la región factible, por ejemplo, si la región factible no está completamente cerrada.
- Solución inviable: si la región factible no existe, el problema no tiene una solución factible.
Por lo general, obtener soluciones inviables o ilimitadas es un indicador de un problema mal definido. En nuestro ejemplo, sin limitar el ancho de la estantería, habríamos conseguido una asignación infinita de libros, aunque no cabrían en las estanterías.
Conclusiones
En esta publicación, nos sumergimos en el mundo de la programación lineal de enteros mixtos para resolver un problema de optimización. Concretamente, modelamos un problema de asignación de productos como ejemplo utilizando la biblioteca de código abierto Pyomo. Modelar los problemas de esta manera es un enfoque poderoso y útil, especialmente cuando hay pocos o ningún dato accesible. La creación de un modelo sólido que represente la realidad suele requerir una comprensión profunda del problema subyacente y cierta experiencia relevante para la industria. Existe mucha bibliografía sobre este tema y la mayoría de los problemas habituales ya se han resuelto. Como primer paso, es una buena práctica consultar una bibliografía especializada antes de intentar reinventar la rueda.








.png)