.png)
Introdução à programação linear de números inteiros mistos (MILP)
Introdução
Hoje em dia, quando pensamos em resolver problemas complexos com computadores, imediatamente pensamos em big data e aprendizado de máquina. O desenvolvimento de uma solução de aprendizado de máquina geralmente requer uma quantidade intensa de dados, que usamos para extrair os padrões e as regras que estão por trás do comportamento de nossos sistemas. Mas o que acontece quando esses dados não são suficientes ou, pior ainda, não há dados disponíveis? Se conhecermos essas regras com antecedência, a Programação Linear de Inteiros Mistos (MILP) pode ser a escolha certa. O MILP é uma subárea da área mais ampla chamada Otimização Convexa e envolve essencialmente duas etapas: modelagem e otimização. Modelar um problema é a arte de expressar um cenário do mundo real como um conjunto de equações e restrições objetivas. O processo de otimização em si está relacionado a encontrar a melhor solução possível para o objetivo, levando em conta as restrições. Pode-se expressar e resolver muitos dos problemas usuais do setor por meio do MILP. Maximizar o fluxo de caixa no setor financeiro, encontrar a rota ideal para um problema de transporte e encontrar uma alocação efetiva de recursos para uma aplicação de manufatura, só para citar alguns. Neste blog, abordamos as aplicações práticas de otimização. Começamos propondo um problema de alocação de produtos e modelando-o usando uma estrutura MILP. Este exemplo também nos permitirá explorar alguns detalhes fundamentais das técnicas MILP e, finalmente, implementaremos o problema modelado em Python usando a biblioteca Pyomo.
Programação linear de números inteiros mistos versus aprendizado de máquina
Embora possamos usar o aprendizado de máquina (ML) e a programação linear de números inteiros mistos (MILP) para resolver alguns dos mesmos problemas (às vezes de forma complementar), a abordagem é bem diferente. O pipeline típico de aprendizado de máquina começa com a coleta e a limpeza de grandes quantidades de dados para depois treinar um modelo que aprende a distribuição subjacente dos dados para explicar o mundo real. Para o MILP, precisamos contar com especialistas para criar um conjunto de regras que explique o mundo real por meio da matemática. À primeira vista, parece que o aprendizado de máquina é uma abordagem superior, pois pode aprender diretamente dos dados. No entanto, quando não temos dados suficientes, temos regras de negócios claramente definidas ou queremos influenciar e modificar o comportamento do nosso sistema de forma transparente, o MILP brilha. Comparando o campo da otimização com os desenvolvimentos de ponta em inteligência artificial, pode-se argumentar que a otimização parece um pouco desatualizada. Desde o final dos anos 70, os matemáticos vêm desenvolvendo a teoria da otimização, especialmente a teoria da Programação Linear de Inteiros Mistos. Embora esses métodos já existam há algum tempo, avanços recentes em algoritmos de otimização e poder computacional bruto tornaram possível resolver grandes problemas de otimização multivariada com milhares (ou talvez milhões) de parâmetros em minutos.
O que podemos resolver com o MILP?
Há uma grande variedade de problemas que podem ser resolvidos com o MILP, vamos nos aprofundar em exemplos rápidos de alguns deles [1]: 💵 Otimização do fluxo de caixa pode ser alcançado escolhendo em quais instrumentos financeiros investir e por quanto tempo, de acordo com nosso capital disponível, para maximizar o retorno ou minimizar o risco. 🛒 Alocação de produtos é o processo de alocar uma variedade de produtos em diferentes prateleiras para maximizar a receita. No exemplo, alocaremos livros de diferentes tamanhos e preços nas prateleiras disponíveis, levando em conta que algumas prateleiras têm mais visibilidade do que outras. 🏭 Alocação de recursos é o processo de alocar estrategicamente os recursos disponíveis para diferentes tarefas. Na fabricação, resolveríamos como alocar os trabalhadores e materiais disponíveis em nossas diferentes linhas de produção para maximizar nosso lucro total ou minimizar o custo total. 🕰️ Agendamento é semelhante à alocação de recursos, mas com a temporalidade levada em consideração. Dado um conjunto de recursos, nós os atribuímos a tarefas em um determinado momento. Por exemplo, se precisarmos designar trabalhadores para turnos, levando em conta sua disponibilidade e habilidades, podemos calcular o melhor cronograma possível. 🛵 Planejamento de rotas é o que toda empresa de entrega de comida faz. Dada uma origem e vários destinos, escolha a melhor rota de acordo com alguns critérios. Minimizar o consumo de combustível, minimizar os prazos médios de entrega ou maximizar o número de itens entregues em um determinado período. ✈️ Redes de transporte são uma das muitas aplicações dos fluxos de rede. Uma empresa de transporte que precisa entregar mercadorias de uma cidade de origem para uma cidade de destino, no entanto, não há voos diretos entre essas cidades. Existem cidades intermediárias que podem conectar indiretamente a origem e o destino, mas os voos têm limites diferentes para a quantidade de mercadorias que podem transportar. Ao modelar esse problema, podemos maximizar o número de mercadorias que chegam ao destino desde a origem.
Princípios básicos do MILP
Nesta seção, vamos nos concentrar nos fundamentos da Programação Linear Inteira Mista. Não entraremos em muitos detalhes matemáticos sobre a formulação, mas forneceremos um contexto geral antes de ir direto para a aplicação. Também definiremos alguns jargões do MILP.
Declaração do problema
Imagine que temos um função objetiva chamado Y precisamos otimizar, por exemplo, o número total de produtos em uma alocação de produtos. Temos um conjunto de parâmetros que contêm informações previamente fixas para o problema, como preços de produtos, tamanhos, dimensões de prateleira e outros valores fixos. Precisamos de algo que possamos ajustar para alcançar o máximo de nossa função objetivo. Para isso, temos variáveis de decisão, que representam qualquer variável livre que precisa ser determinada ao resolver o problema e são indicadas com a letra x. Por exemplo, as posições de cada um de nossos produtos. Os valores possíveis para as variáveis de decisão devem verificar um conjunto de condições externas lineares denominadas restrições. Se tivermos M restrições que dependem linearmente das variáveis de decisão, podemos formular o problema da seguinte forma [2]:
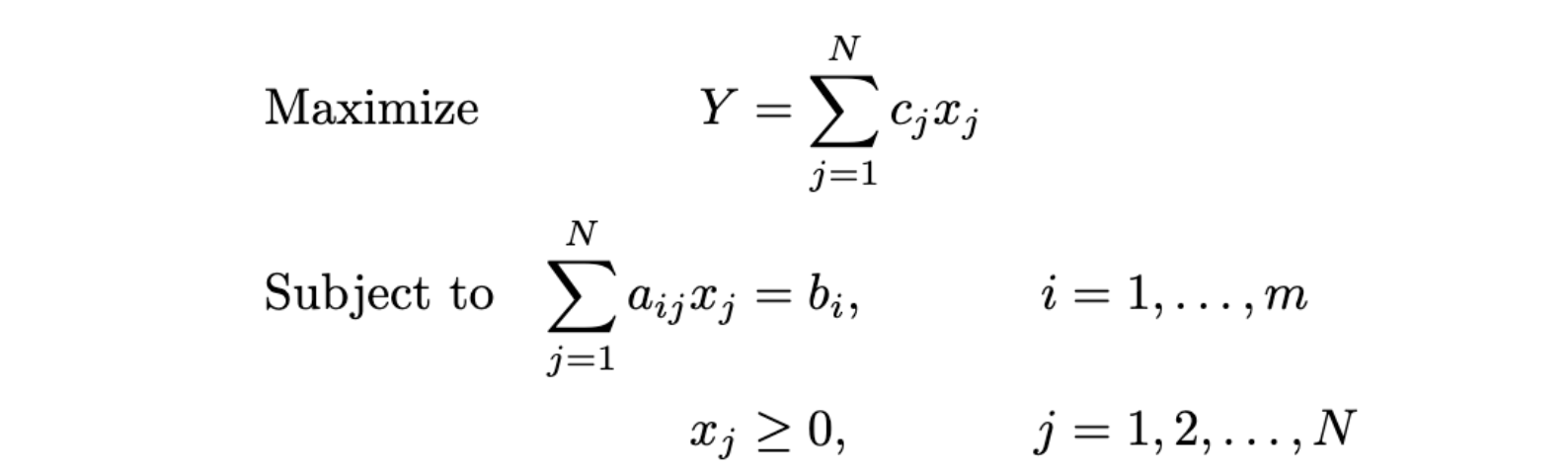
Resolver esse problema envolve encontrar um conjunto de valores x que maximiza (ou minimiza) o resultado Y. As restrições podem ser igualdades ou desigualdades e poderíamos ter um número arbitrário delas. Conforme mencionado anteriormente, essa estrutura pode modelar uma ampla variedade de problemas em diferentes setores. O sucesso nessa área depende da capacidade de traduzir cenários do mundo real em conjuntos de equações. Em seguida, aplicamos essa estrutura a um problema de alocação de produtos.
Programação não linear
Essa formulação MILP pode ser estendida para outras áreas da Pesquisa Operacional. Se algumas das restrições, ou mesmo a função objetivo, incluírem alguma não linearidade, ainda é possível resolver o problema de otimização. Isso requer a aplicação de um conjunto diferente de técnicas, conhecido como Programação Não Linear de Inteiros Mistos (MINLP). No entanto, também se pode usar técnicas tradicionais de MILP aproximando variáveis não lineares linearizando-as no intervalo de interesse. Isso logicamente levaria a soluções aproximadas, mas, na maioria dos casos, essas soluções são boas o suficiente para os problemas do aplicativo.
Otimização na prática: alocação de produtos
Uma livraria on-line quer abrir sua primeira loja física, e um dos desafios que ela enfrenta é como colocar livros nas estantes para maximizar a receita. Para resolver isso, eles optaram por entrar em contato conosco, assistentes de otimização, para ajudar a resolver o problema. Resumimos seus requisitos na seguinte declaração: Precisamos colocar o máximo de livros possível nas estantes, colocando os livros mais populares nas prateleiras mais visíveis e mantendo os mesmos autores juntos. Conforme mencionado na seção anterior, precisamos identificar parâmetros, variáveis, restrições e função objetivo, para que possamos então encontrar a solução ideal. É prática comum definir esses componentes da solução verbalmente para depois formulá-los matematicamente. Parâmetros: Para cada livro, precisamos medir sua popularidade, preço, autor e dimensões. Por sua vez, para cada prateleira dentro das estantes de livros, precisamos conhecer as dimensões e a visibilidade ou exposição que elas fornecem aos livros. Variáveis: Para cada livro, precisamos saber em qual prateleira e em qual lugar dentro dessa prateleira ele deve estar localizado. Restrições: Devemos incluir apenas uma cópia de cada livro e eles devem caber na prateleira por altura. O comprimento total dos livros selecionados em uma prateleira deve caber na largura da estante. Além disso, livros do mesmo autor devem estar na mesma estante. Função objetiva: A receita de cada livro é definida pelo preço do livro, sua popularidade e a visibilidade que sua localização oferece. Nosso objetivo é maximizar a receita total, como a soma da receita de todos os livros alocados.
Conjuntos
Primeiro, definimos o conjunto de índices que usaremos para definir nosso problema. Como teremos muitas variáveis e parâmetros que se repetem para cada livro, estante e autor, os índices facilitam muito a notação.
- O conjunto B representa o conjunto de livros considerados para o problema. Cada livro individual será referenciado com o subíndice b.
- O conjunto C representa o conjunto de estantes consideradas para o problema. Cada estante individual será referenciada com o subíndice c.
- O conjunto UM representa o conjunto de autores considerados para o problema. Cada autor individual será referenciado com o subíndice a.
- O conjunto S representa o conjunto de prateleiras considerado para o problema. Cada prateleira individual será referenciada com o subíndice s.
Parâmetros
Em seguida, definimos os parâmetros do problema, que representam informações e configurações anteriores, ou seja, valores que não podemos ajustar em nosso processo de otimização:
Livros
- Nós definimos o parâmetro b_popb como a popularidade do livro b.
- Nós definimos o parâmetro b_widthp como a largura em mm para o livro b.
- Nós definimos o parâmetro b_alturab como a altura em mm para o livro b.
- Nós definimos o parâmetro b_priceb como o preço em USD do livro b.
- Definimos o parâmetro booleano é_autora, b o que é verdade se o livro b foi escrito pelo autor uma e falso se não.
Estantes
- Nós definimos o parâmetro s_largurac, s como a largura em mm para prateleira s da estante c.
- Nós definimos o parâmetro s_heightc, s como a altura em mm para prateleira s da estante c.
- Nós definimos os parâmetros s_visibilidadec, s como a visibilidade que um livro ganha ao ser posicionado na prateleira b da estante c.
Variáveis de decisão
Em seguida, devemos identificar as variáveis de decisão cujos valores devem ser encontrados no processo de otimização. Essas variáveis representam todos os valores que podemos ajustar como profissionais:
- Definimos a variável booleana Is_Book_Atb, c, s que representa se um livro b está na prateleira s de estante c.
- Definimos a variável booleana Is_Author_Ata, c, s que representa se o autor uma está na prateleira s de estante c.
Restrições
Agora, tendo definido as variáveis de decisão, precisamos definir matematicamente todas as restrições do problema. Nossa primeira restrição está relacionada à limitação do número de vezes que podemos alocar um livro.
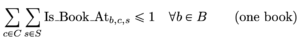
Dessa forma, garantimos que cada livro seja alocado no máximo uma vez, permitindo também que o modelo omita livros se eles não couberem. Duas restrições têm a ver com o tamanho das prateleiras:


Para limitar o número de estantes em que um autor aparece, precisamos preencher a variável acessória Is_Author_Ata, c, s. Isso pode ser feito pela combinação de duas restrições.
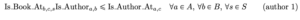
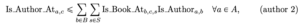
Em seguida, precisamos garantir que cada autor apareça em no máximo uma estante de livros:

Função objetiva
Finalmente, precisamos definir a função objetivo que estamos tentando maximizar. Nesse caso, a receita esperada de uma disposição específica de livros:

Depois de formular o problema, resolvê-lo se torna uma questão de utilizar solucionadores de programação linear padrão. Existem muitos solucionadores de código aberto, como GLPK do GNU, GLOP, e CP-SAT desenvolvido pelo Google e muito mais.
Otimização da alocação de produtos usando Pyomo
Agora que o problema está completamente definido, é hora de implementá-lo usando Pyomo [3], uma biblioteca de código aberto baseada em Python que oferece suporte a um conjunto diversificado de recursos de otimização para resolver modelos de otimização. Embora o utilizemos para resolver um problema linear, ele também tem recursos não lineares para resolver problemas mais complexos. Agora é hora de começar a encher nossas estantes!

Conjunto de dados
Para resolver nosso problema, precisamos dos dados do livro. Trabalharemos com um conjunto de dados de livros de fantasia (inspirados neste conjunto de dados). Ele inclui recursos do livro, como dimensões, informações sobre o autor e vendas médias. A popularidade de um livro pode ser inferida pela média de suas vendas. Em seguida, precisamos medir nossas estantes imaginárias para definir o espaço disponível para livros. Neste exemplo, trabalharemos com 3 estantes de livros, 5 prateleiras cada, com 1 metro de largura e altura suficiente para guardar as mais altas. Cada prateleira também tem seu próprio fator de visibilidade, um multiplicador nas vendas de livros à medida que os posicionamos nessa prateleira. Vamos dar uma olhada nos dados que forneceremos ao modelo.

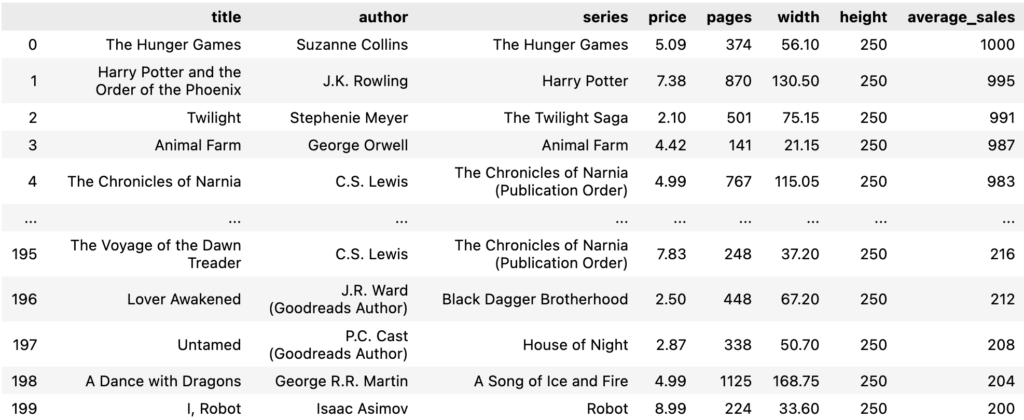
modelo
Parâmetros
Uma característica interessante do Pyomo é que ele nos permite definir variáveis e parâmetros do modelo de forma funcional. Usando a notação definida na seção anterior, temos nossos conjuntos: # Defina os conjuntos Model.b = pyo.set (initialize=book_ids, doc="books”) model.S = pyo.Set (initialize=shelf_ids, doc="Shelves”) Model.c = pyo.set (initialize=bookcase_ids, doc="Bookcases”) Model.a = pyo.set (initialize=author_ids, doc="Authors”) E nossos parâmetros: # Defina os parâmetros model.b_width = pyo.param (model.B, initialize=lambda model, b: book_widths [b], within=pyo.nonnegativeReals, doc="width of book b”,) model.b_height = pyo.param (model.B, initialize=lambda modelo, b: book_heights [b], within=pyo.nonnegativeReals, doc="Altura do livro b”,) model.b_pop = pyo.param (model.b, initialize=lambda model, b: book_average_sales [b], within=pyo.nonnegativeReals, doc="Average sales of book b”,) model.b_price = pyo.param (model.B, initialize="Average sales of book b”,) model.b_price = pyo.param (model.B, initialize="Average sales of book b” lambda model, b: book_prices [b], within=pyo.nonnegativeReals, doc="Price of book b”,) model.is_author = pyo.param (model.B, model.A, initialize=lambda model, b, a: 1 if author_per_book [b] == a else 0, within=pyo.binary, doc="É autor do livro b”, model.s_height = pyo.param (model.s, model.C, initialize=lambda model, s, c: shelf_heights [c, s], within=pyo.nonnegativeReals, doc="Altura da prateleira s na estante c”,) model.s_width = pyo.param (model.s, model.C, initialize=lambda model, s, c: shelf_widths [c, s], within=pyo.nonnegativeReals, doc="Largura da prateleira s na estante c”,) model.s_visibility_factor = pyo.param (model.s, model.C, initialize=lambda model, s, c: shelf_visibility_factor [s], doc="Fator de visibilidade da prateleira s na estante c”,) Dessa forma, estamos dizendo ao Pyomo que larguras e alturas são parâmetros com componentes B e que a prateleira tem parâmetros S vezes C componentes, um para cada prateleira em cada estante. Essa formulação é bastante útil, pois permite modificar a dimensão da entrada sem alterar esse trecho de código.
Variáveis de decisão
Agora, definimos as variáveis de decisão e forçamos nossas variáveis de decisão a serem binárias. # Defina as variáveis model.is_book_at = pyo.var (model.B, model.S, model.C, domain=pyo.binary) Model.is_author_at = pyo.var (model.A, model.C, domain=pyo.binary)
Restrições
Em seguida, adicionamos todas as restrições ao modelo. No Pyomo, é possível definir as restrições usando funções regulares do Python. Essas funções devem retornar um valor booleano com base em uma condição nos parâmetros e variáveis. Primeiro definimos todas as funções: def __width_rule (model, s, c): return (sum (model.is_book_at [b, s, c] * model.b_width [b] for b in Model.b) <= model.s_width [s, c]) def __height_rule (model, s, b, c): return (model.is_book_at [b, s, c] * model.b_height [b] <= model.s_height [s, c]) def __max_books_rule (model, b): soma de retorno (model.is_book_at [b, s, c] para s nos modelos.S para c no modelo.C) <= 1 def __author_in_bookshelve_rule_1 (model, b, a, s, c): return (Model.is_author_at [a, c] >= Model.is_book_at [b, s, c] * model.is_author [b, a]) def __author_in_bookshelve_rule_2 (model, a, c): retorna Model.is_author_at [a, c] <= sum (Model.is_book_at [b, s, c] * model.is_author [b, a] para b em Model.b para s em Model.s) def __max_bookshelves_author_rule (model, a): retorna sum (Model.is_author_at [a, c] para c em Model.s c) <= 1 E então defina as restrições: # Defina as restrições model.width_constraint = pyo.Constraint (model.s, model.C, rule=width_rule, doc = “Todos os livros na prateleira juntos devem ter menos que a largura da prateleira”) model.height_constraint = pyo.Constraint (Model.s, Model.b, model.C, rule=height_rule, doc = “Os livros devem ter menos altura do que a altura da prateleira” ) model.max_books_constraint = pyo.constraint (model.B, rule=max_books_rule, doc = “Cada livro deve estar em apenas uma prateleira”) model.author_in_bookshelve_constraint_1 = pyo.Constraint (model.B, model.A, model.S, model.C, rule=author_in_bookshelve_rule_1, doc = “Preencha se o autor estiver na estante”) model.author_in_bookshelve_constraint_2 = pyo.Constraint (model.A, model.C, rule=author_in_bookshelve_rule_2, doc = “Preencha se o autor estiver na estante”) model.max_bookshelves_author_constraint = pyo.Constraint (model.A, rule=max_bookshelves_author_rule, doc = “Cada autor deve estar em apenas uma estante de livros”)
Função objetiva
O ingrediente final em nosso modelo é a função objetivo. # Função objetiva def objective_function (model): total_books_earnings = sum (model.is_book_at [b, s, c] * model.b_price [b] * model.b_pop [b] * model.s_visibility_factor [s, c] para b no modelo.B para s nos modelos.B para c no modelo.S para c no modelo.B .c) return total_books_earnings model.cost = pyo.Objective (rule=objective_function, sense=pyo.maximize)
Resolvendo o modelo
Agora podemos finalmente resolver o modelo: # Selecione solver and solve solver = pyo.SolverFactory ('glpk') solution = solver.solve (model) Vamos verificar como nos saímos na modelagem do problema. A imagem abaixo mostra como os livros estavam localizados nas estantes. Em laranja, destacamos os livros de J.K Rowling, para mostrar que os livros do mesmo autor estão na mesma estante.

Podemos ver que os livros se encaixam bem nas estantes, com pouco ou nenhum espaço de sobra. Além disso, livros finos com largura/preços mais altos estão localizados nas prateleiras do meio, as regiões mais visíveis da estante, enquanto livros mais grossos e mais baratos estão localizados nas prateleiras inferiores. A tabela a seguir resume algumas estatísticas sobre os resultados.
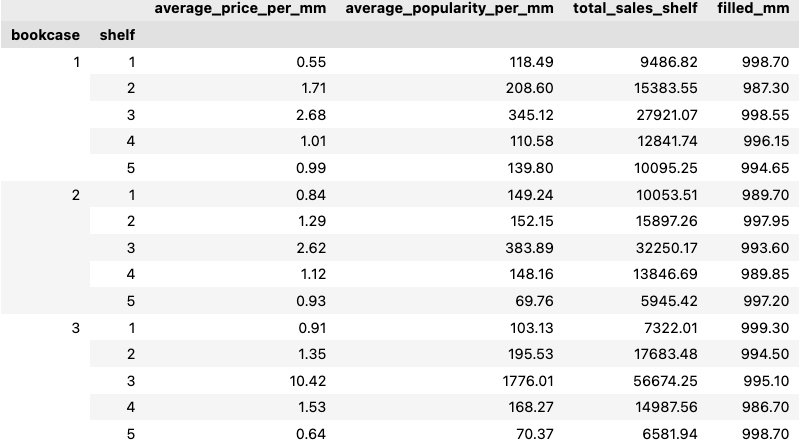
O que aconteceria se tivéssemos menos livros? Vamos executar o modelo novamente, mas remover alguns dos livros menos populares da lista de entradas.

Como esperado, o modelo opta por deixar espaços vazios em uma das prateleiras menos visíveis. Colocar um livro lá em vez de em uma prateleira com maior visibilidade iria contra o objetivo do modelo.
Sempre podemos obter uma solução ideal?
Ao analisar as formulações de LP ou MILP, vemos que as restrições impõem algumas restrições aos valores possíveis para as variáveis de decisão. Existem combinações de valores que não atenderão às restrições e, portanto, não serão os candidatos ideais. Formalmente, pode-se avaliar a viabilidade do problema de otimização para MILP com as condições de Karush—Kuhn—Tucker (KKT). Por uma questão de simplicidade, não abordaremos isso neste post. O conjunto de todas as combinações de variáveis de decisão que satisfazem todas as restrições é chamado de região viável, e resolver um problema de programação linear envolve encontrar o valor máximo (ou mínimo) de uma função objetivo dentro dessa região viável.
Soluções viáveis e limitadas
Para visualizar essa região viável, imagine que temos duas variáveis de decisão não negativas x1 e x2 e um conjunto de restrições. Poderíamos representar o problema em um gráfico bidimensional conforme abaixo: [caption id="attachment_3102" align="aligncenter” width="350"]
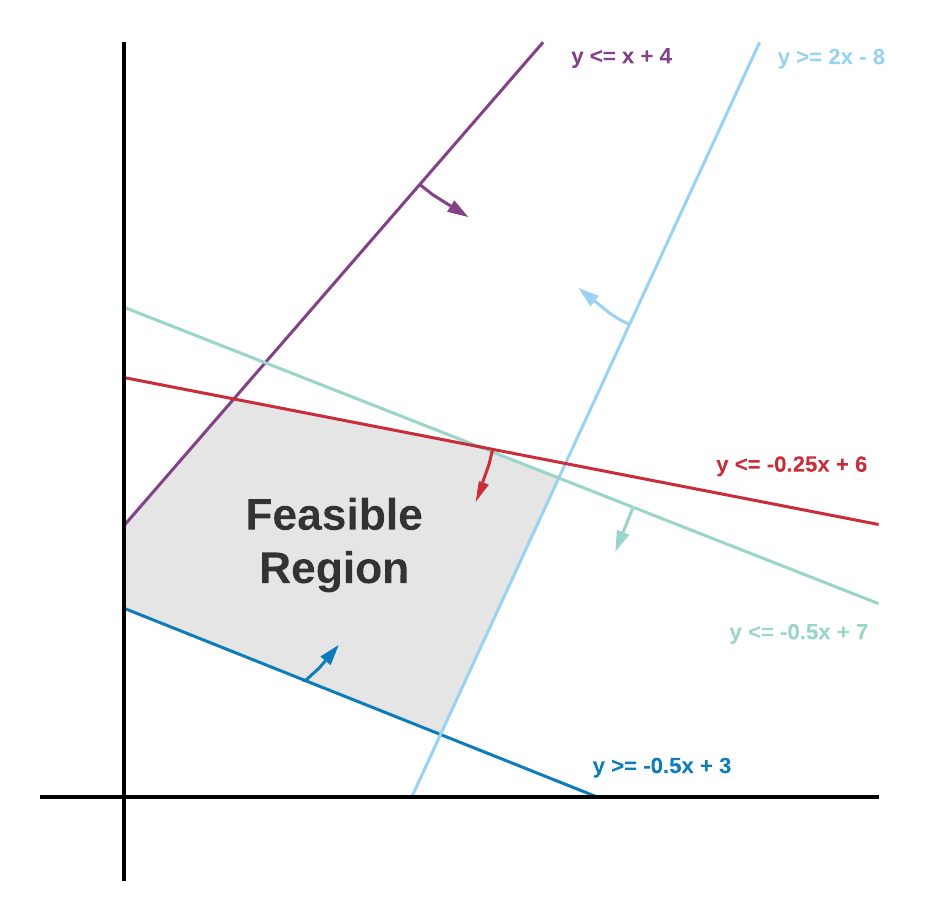
Delimitação de uma região viável [4][/caption] A região viável nesse caso é a região sombreada em cinza, que representa todas as combinações possíveis de x1 e x2 que satisfazem todas as restrições ao mesmo tempo. Os valores ideais para a função objetivo estarão em um dos vértices ou bordas da região viável. Portanto, a essência da solução de um problema de programação linear é procurar os valores objetivos nesses pontos.
Soluções inviáveis ou ilimitadas
Nosso problema pode envolver uma solução viável limitada, como na imagem acima, mas essa região também pode ser inviável ou ilimitada. Regiões inviáveis aparecem quando não há uma combinação de variáveis que possa satisfazer todas as restrições ao mesmo tempo. Regiões ilimitadas aparecem quando a área viável é infinitamente grande. A imagem abaixo mostra a diferença entre esses cenários: [caption id="attachment_3093" align="aligncenter” width="788"]
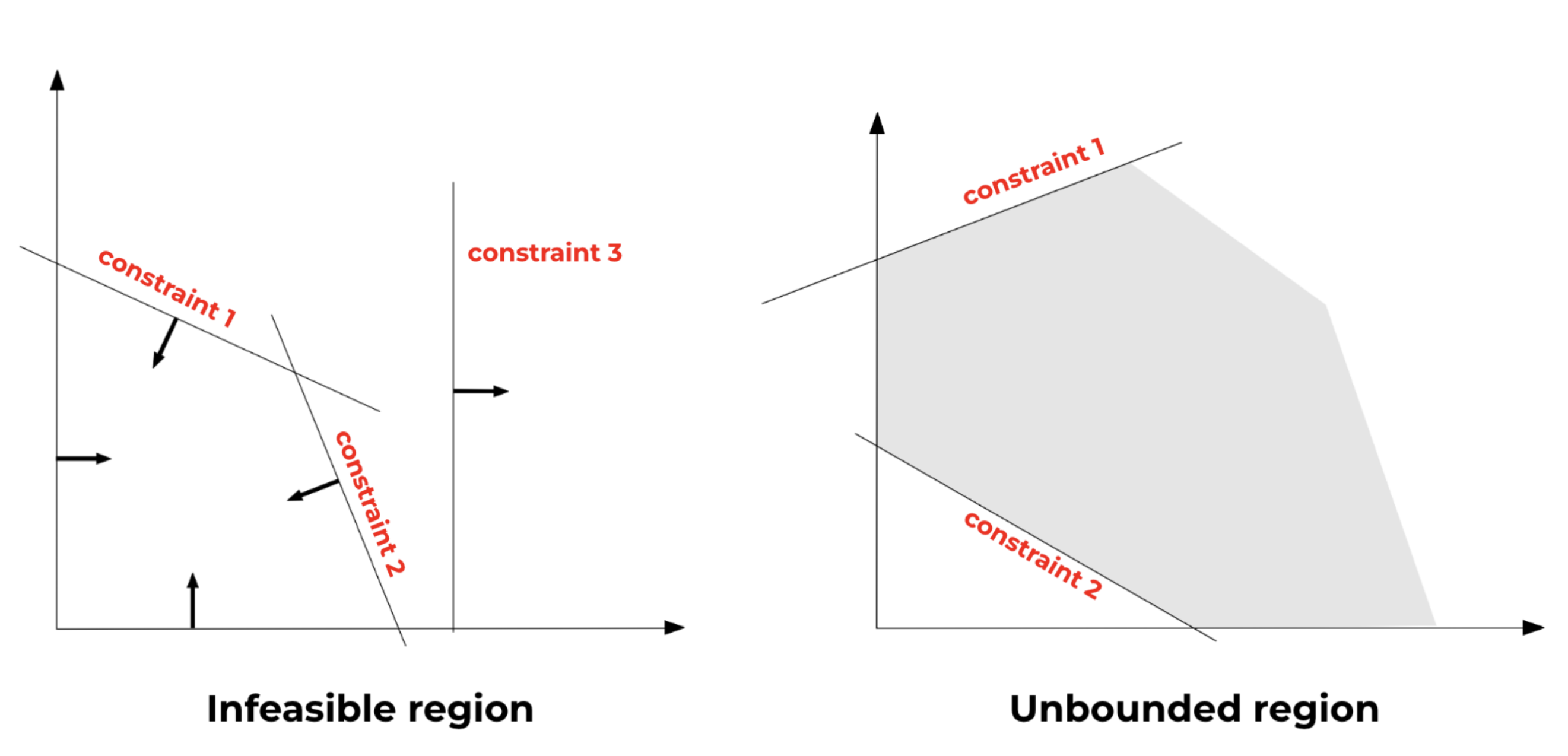
Imagem adaptada do manual de modelagem de otimização AIMMS [5][/caption] Dependendo do forma da região viável, o problema pode ter uma solução ou não, e podemos categorizar a solução do problema em três cenários diferentes:
- Solução ideal: nesse caso, o problema está bem definido e é possível encontrar um valor ótimo da função objetivo dentro da região viável.
- Solução ilimitada: sempre que a função de maximizar (minimizar) pode crescer (diminuir) infinitamente dentro da região viável, por exemplo, se a região viável não estiver completamente fechada.
- Solução inviável: se a região viável não existe, o problema não tem uma solução viável.
Normalmente, obter soluções inviáveis ou ilimitadas é um indicador de um problema mal definido. Em nosso exemplo, sem limitar a largura da estante, teríamos alcançado uma alocação infinita de livros, embora eles não cabessem nas prateleiras.
Conclusões
Neste post, mergulhamos no mundo da programação linear de números inteiros mistos para resolver um problema de otimização. Especificamente, modelamos um problema de alocação de produtos como exemplo usando a biblioteca de código aberto Pyomo. Modelar problemas dessa forma é uma abordagem poderosa e útil, especialmente quando poucos ou nenhum dado está acessível. A criação de um modelo robusto que represente a realidade geralmente requer uma compreensão profunda do problema subjacente e alguma experiência relevante para o setor. Existe muita bibliografia sobre esse tópico e a maioria dos problemas usuais já foi resolvida. Como primeiro passo, é uma boa prática consultar uma bibliografia especializada antes de tentar reinventar a roda.








.png)