Introducción

Imagina un mundo en el que la creatividad trascienda las limitaciones de los pinceles, la arcilla y el lienzo. Fue en 2022, en el concurso de arte de la Feria Estatal de Colorado, cuando una obra innovadora desafió los límites convencionales de la creación artística. La obra maestra de Jason M. Allen, «Théâtre d'Opéra Spatial» ganó el primer premio y desafió las convenciones. No por medios tradicionales, sino con la ayuda de un programa de inteligencia artificial llamado A mitad del viaje, que utiliza un modelo de difusión para generar imágenes. Al convertir un mensaje de texto en una imagen hiperrealista, la creación de Allen no solo cautivó al público y a los jueces, sino que también provocó una fuerte reacción por parte de los artistas que lo acusaron, básicamente, de hacer trampa.

Entrada del «Théâtre d'Opéra Spatial» para la Feria Estatal de Colorado.

Sin embargo, el auge de Midjourney y otros avances de la IA no hacen más que rayar la superficie de lo que es posible con los modelos de difusión. Estos modelos generativos se han convertido en una fuerza a tener en cuenta, ya que atraen la atención y amplían los límites de la síntesis de imágenes por los que antes se regía Redes generativas de confrontación (GAN) [1]. De hecho, se dice que los modelos de difusión son superar a las GAN en la síntesis de imágenes [2]. En este artículo, exploramos los fundamentos teóricos de los modelos de difusión, descubriendo su funcionamiento interno y comprendiendo sus componentes fundamentales y su notable eficacia. A lo largo del camino, nos centraremos en una de las familias de modelos de difusión más populares: la difusión estable. Únase a nosotros para descubrir los secretos del éxito de los modelos de difusión y cómo están revolucionando la generación de imágenes. Al final, comprenderás en profundidad su potencial transformador, que inspirará el ámbito de la creatividad impulsada por la inteligencia artificial.

Modelos de difusión

Los modelos de difusión son modelos generativos que aprenden de los datos durante el entrenamiento y generan ejemplos similares en función de lo que han aprendido. Estos modelos se inspiran en la termodinámica del desequilibrio y han alcanzado una calidad de vanguardia en la generación de diversas formas de datos. Algunos ejemplos incluyen la generación de imágenes e incluso audio de alta calidad (p. ej. Modelos de difusión de audio [3]). Si está interesado en saber cómo se pueden aplicar los modelos de difusión en la configuración de audio, consulte nuestro blog sobre clonación de voz. En pocas palabras, los modelos de difusión funcionan corrompiendo los datos de entrenamiento mediante la adición de ruido gaussiano (llamado proceso de difusión directa) y, a continuación, aprender a recuperar la información original invirtiendo este proceso de generación de ruido paso a paso (denominado proceso de difusión inversa). Una vez entrenados, estos modelos pueden generar nuevos datos muestreando ruido gaussiano aleatorio y pasándolo por el proceso aprendido de eliminación de ruido. Los modelos de difusión van más allá de la simple creación de imágenes de alta calidad. Han ganado popularidad al abordar los conocidos desafíos asociados con el entrenamiento contradictorio en las GAN. Los modelos de difusión ofrecen ventajas en términos de estabilidad de entrenamiento, eficiencia, escalabilidad, y paralelización. En las siguientes secciones, profundizaremos en los detalles de los modelos de difusión. Exploraremos los proceso de difusión directa, el proceso de difusión inversa, y una descripción general de las etapas del proceso de formación. Además, también obtendremos una intuición sobre el cálculo del función de pérdida. Al examinar estos componentes, adquiriremos una comprensión completa de cómo funcionan los modelos de difusión y cómo logran sus impresionantes resultados.

Proceso de difusión directa

El proceso de difusión directa consiste en añadir gradualmente ruido gaussiano a una imagen de entrada paso a paso, para un total de T escalones. En el paso 0 tenemos la imagen original, en el paso 1 una imagen ligeramente dañada que se corrompe aún más paso a paso hasta que se pierde toda la información de la imagen original.

Proceso de difusión directa [4]

Para formalizar este proceso, podemos verlo como algo fijo Cadena Markov con T pasos, donde la imagen en el paso del tiempo t se asigna a su estado posterior en el paso del tiempo t+1. Por lo tanto, cada paso depende únicamente del anterior, lo que nos permite derivar una fórmula de formato cerrado para obtener la imagen dañada en cualquier intervalo de tiempo deseado, sin necesidad de realizar cálculos iterativos.

Formulación de difusión directa [4]

En consecuencia, esta fórmula de forma cerrada permite el muestreo directo de xen cualquier paso de tiempo, lo que acelera significativamente el proceso de difusión directa.

Programadores

Además, la adición de ruido en cada paso sigue un patrón deliberado. A Planificador determina la cantidad de ruido que se añadirá. En el original Documento sobre modelos probabilísticos de difusión (DDPM) sobre la eliminación de ruido [4], los autores definen un cronograma lineal que varía β de 0,0001 en el paso temporal 0 a 0,02 en el paso temporal T. Sin embargo, varias alternativas ganaron popularidad, como el calendario de cosenos introducido en el Documento sobre modelos probabilísticos de difusión de ruido mejorados [5]. Por ejemplo, la siguiente imagen muestra la diferencia entre usar un cronograma lineal y un cronograma de coseno para el proceso de difusión directa. En la primera fila se muestra un cronograma lineal, mientras que en la segunda fila se muestra el cronograma de cosenos mejorado.

Programadores lineales y de coseno, extraídos del documento DDPM mejorado [5]

Los autores del artículo sobre DDPM mejorado sostienen que el cronograma de cosenos ofrece un rendimiento superior. Un cronograma lineal puede provocar una pérdida rápida de información en la imagen de entrada. Como resultado, esto generalmente conduce a un proceso de difusión abrupto. Por el contrario, el programa del coseno proporciona una degradación más suave. Por lo tanto, permite que los pasos posteriores funcionen en imágenes que no estén completamente saturadas por el ruido.

Proceso de difusión inversa

A la inversa del proceso de difusión directa, el proceso de difusión inversa plantea un desafío computacional, ya que la formulación de q (x|x) se vuelve intratable o incomputable. Para abordar los desafíos del proceso de difusión inversa, los modelos de aprendizaje profundo pasan a ser el centro de atención y aproximan este elusivo proceso de difusión inversa con una red neuronal.

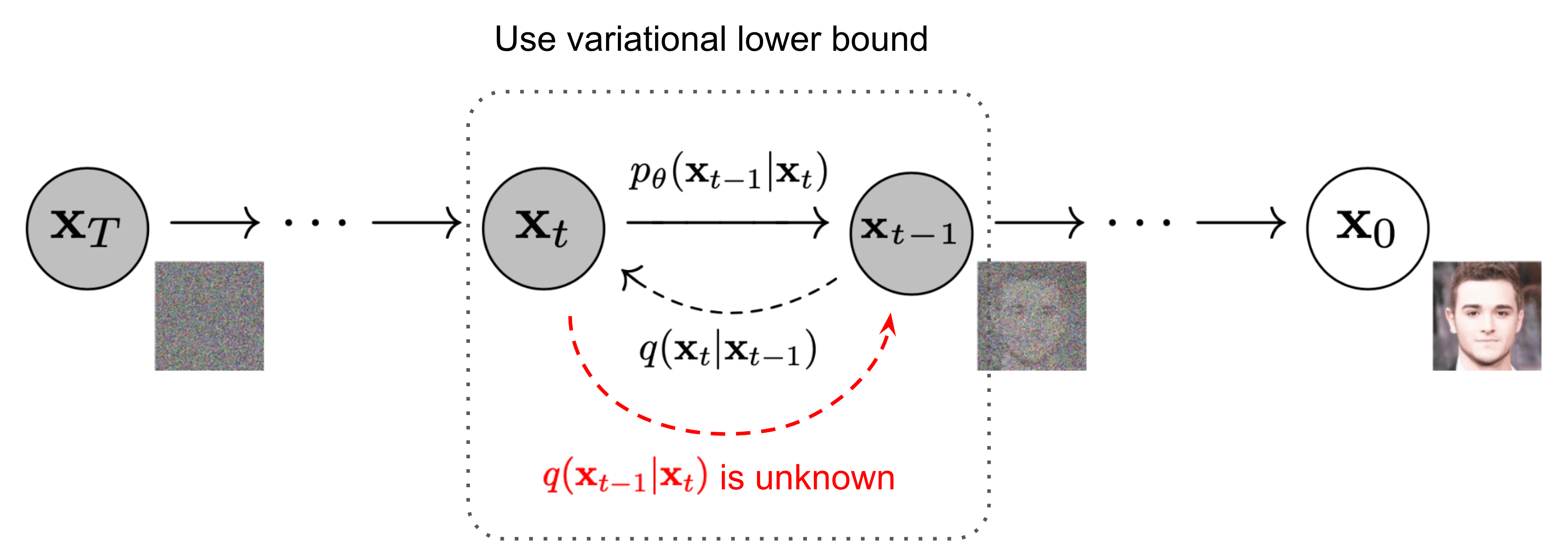
Proceso de difusión inversa [6]

En términos generales, la función de esta red neuronal es predecir todo el ruido presente en la imagen en un determinado período de tiempo. t. Luego, al comparar esta predicción con el ruido real agregado a la imagen, se puede entrenar la red. En el momento de la inferencia, estas redes siguen prediciendo todo el ruido presente en la imagen en el intervalo temporal t, y luego simplemente elimine una fracción del ruido presente según el planificador utilizado. Como resultado, al predecir el ruido en el paso temporal t, podemos caer en la tentación de intentar recuperar la imagen original en un solo paso. Sin embargo, algunos experimentos empíricos han demostrado que se necesitan pasos más pequeños para lograr una mayor estabilidad. De ahí la necesidad de eliminar solo una fracción del ruido presente en la imagen en la etapa temporal t para obtener la imagen en la etapa temporal t-1. Algunos artículos y blogs pueden ser engañosos en el sentido de que, al leerlos, la gente tiende a creer que la red predice el ruido añadido por Timestep t-1 a timestep T.AAunque esto se puede aclarar consultando el código proporcionado por sus autores.

Arquitectura de redes neuronales

Quizás se pregunte acerca de la arquitectura de esta red neuronal. En términos generales, los modelos de difusión utilizan algún tipo de variante U-Net para aproximar el proceso de difusión inversa. Esta elección se debe a la popularidad de U-Net en la comunidad de visión artificial. Además, parece una excelente opción teniendo en cuenta que el único requisito es que la entrada y la salida del modelo de difusión deben mantener una dimensionalidad idéntica, excepto en los modelos de difusión de superresolución [7].

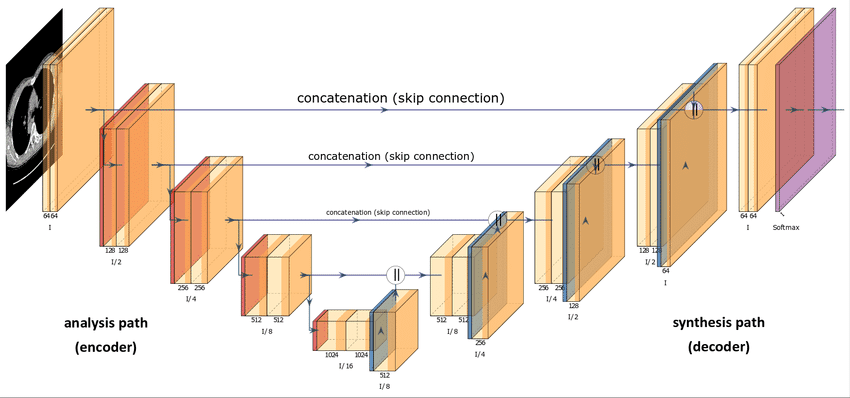
Arquitectura U-Net [8]

En cuanto a los detalles de implementación descritos en el documento DDPM, las principales opciones de arquitectura incluyen:

• El codificador y decodificador las rutas tienen el mismo número de niveles e incorporan un bloque de cuello de botella entre ellas.
• Cada etapa del codificador consiste en dos bloques residuales con submuestreo convolucional, excepto en el nivel final.
• Cada etapa del decodificador consiste en tres bloques residuales. Además, los autores definen x2 bloques de muestreo ascendente del vecino más cercano con convoluciones para restaurar la entrada del nivel anterior.
• La ruta del decodificador se conecta a cada etapa de la ruta del codificador a través de omitir conexiones.
• El uso de módulos de atención con una resolución de mapa de características única dentro del modelo.
• Además, el intervalo de tiempo t está codificado en un incrustación temporal. Esto es bastante similar al Codificación posicional sinusoidal presentado en el Papel transformador [9].

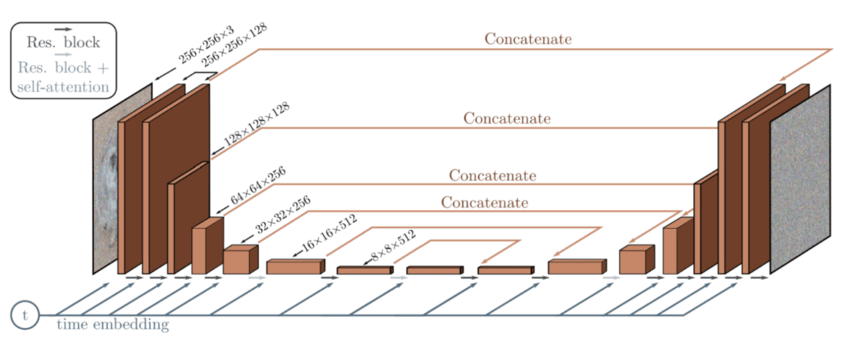
Arquitectura del modelo de difusión basada en la U-Net [10]

Estas incrustaciones temporales ayudan a la red neuronal a obtener cierta información sobre en qué estado (paso) se encuentra la imagen actualmente. Esto es útil para saber si hay más o menos ruido en la imagen, lo que hace que el modelo reste más o menos ruido. En términos generales, en intervalos de tiempo más bajos, el proceso de difusión hacia adelante añade menos ruido que en intervalos de tiempo más altos. Como ejemplo, así es como se ve todo el proceso de difusión avance/inversa:

Proceso de difusión directa e inversa [11]

Cálculo de pérdidas

Para entrenar un modelo de difusión, el objetivo es encontrar las transiciones inversas de Markov que maximicen la probabilidad de obtener los datos de entrenamiento. Esto equivale a minimizar la Límite inferior variacional (VLB) sobre la probabilidad logarítmica negativa. Aunque se denomina límite inferior, técnicamente es un límite superior, el negativo del Evidence Lower Bound (ELBO). Sin embargo, nos ceñimos a la literatura de referencia para mantener la coherencia en las diferentes fuentes. En la práctica, maximizar la probabilidad se traduce en minimizar la probabilidad logarítmica negativa

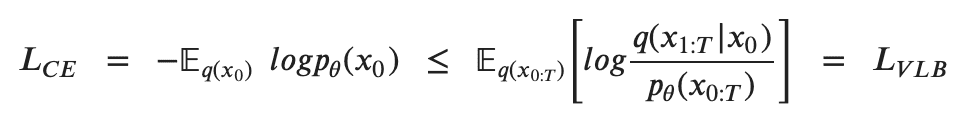
La desigualdad de Jensen para minimizar la entropía cruzada como objetivo de aprendizaje [6]

Para convertir cada término de la ecuación para que sea computable analíticamente, el objetivo se puede reescribir aún más para que sea una combinación de varios Divergencia KL y términos de entropía [12]. Además, para ver una formulación paso a paso más detallada, visite El blog de Lilian Weng[6] sobre modelos de difusión.

Reformulación con KL Divergence

La divergencia KL mide la distancia estadística asimétrica entre distribuciones de probabilidad, cuantificando en qué medida una distribución P difiere de una distribución de referencia Q. Es conveniente formular el VLB en términos de divergencias KL, ya que las distribuciones de transición en la cadena de Markov son gaussianas y la divergencia KL entre gaussianas tiene una forma cerrada. La representación matemática de la divergencia KL para distribuciones continuas es:

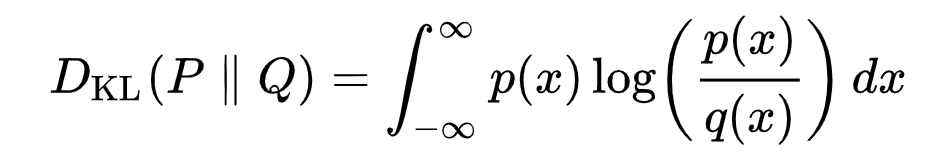
Formulación de KL Divergence [13]

Pero, ¿cómo se ve esto en la práctica? Proporcionamos un gráfico de ejemplo que ilustra la divergencia KL de una distribución variable P (distribución azul) con respecto a una distribución de referencia Q (distribución roja). La curva verde representa la función dentro de la integral en la definición de la divergencia KL, y el área total bajo la curva representa el valor de la divergencia KL de P de Q en un momento específico, mostrado numéricamente.

KL Representación de divergencia para dos distribuciones determinadas: Q (distribución de referencia) y P (distribución variable) [13]

La divergencia KL compara las distribuciones gaussianas en el proceso de entrenamiento de la difusión: la distribución de referencia de la difusión directa con el ruido gaussiano añadido y el ruido previsto durante la difusión inversa.

No profundizaremos en las matemáticas de Diffusion Models. Sin embargo, esperamos que esto ayude a tener una visión general de cómo estos modelos calculan las pérdidas y actualizan sus parámetros. El modelo predice el ruido en un período de tiempo específico t, utilizando la desviación estándar fija y la media real a partir de la difusión directa, junto con la desviación media y estándar del ruido añadido. Calculamos la divergencia KL de las imágenes en estas distribuciones. Este cálculo abarca todas las imágenes del lote, lo que facilita la retropropagación de las redes neuronales.

Proceso de formación

En cada fase del proceso de formación, se siguen los siguientes pasos:

1. Muestreo de un intervalo de tiempo aleatorio t para cada muestra de entrenamiento del lote (por ejemplo, imágenes)
2. Agregar ruido gaussiano mediante la fórmula de forma cerrada, de acuerdo con sus pasos de tiempo t
3. Convertir los pasos temporales en incrustaciones para alimentar la U-Net o modelos similares (u otra familia de modelos)
4. Uso de las imágenes con incrustaciones de ruido y tiempo como entrada para predecir el ruido presente en las imágenes
5. Comparación del ruido previsto con el ruido real para calcular la función de pérdida
6. Actualización de los parámetros del modelo de difusión mediante retropropagación mediante la función de pérdida

Este proceso se repite en cada época, utilizando las mismas imágenes. Sin embargo, normalmente se toman muestras de diferentes intervalos de tiempo para cada imagen en épocas diferentes. Esto permite que el modelo aprenda a invertir el proceso de difusión en cualquier momento, lo que mejora su adaptabilidad

Representación de las imágenes corruptas en un lote fijo durante diferentes épocas durante el entrenamiento [14]

Proceso de muestreo

Para muestrear imágenes nuevas, la diferencia radica en que no tenemos una imagen de entrada. Tomamos muestras de ruido gaussiano aleatorio y definimos cuántos pasos de ruido (T) debemos tomar para generar las nuevas imágenes. En cada paso, el modelo de difusión predice todo el ruido presente en la imagen, tomando como entrada el intervalo de tiempo actual. Luego, elimina solo una fracción de este ruido previsto. Obtenemos el resultado de la generación de imágenes después de T pasos de inferencia.

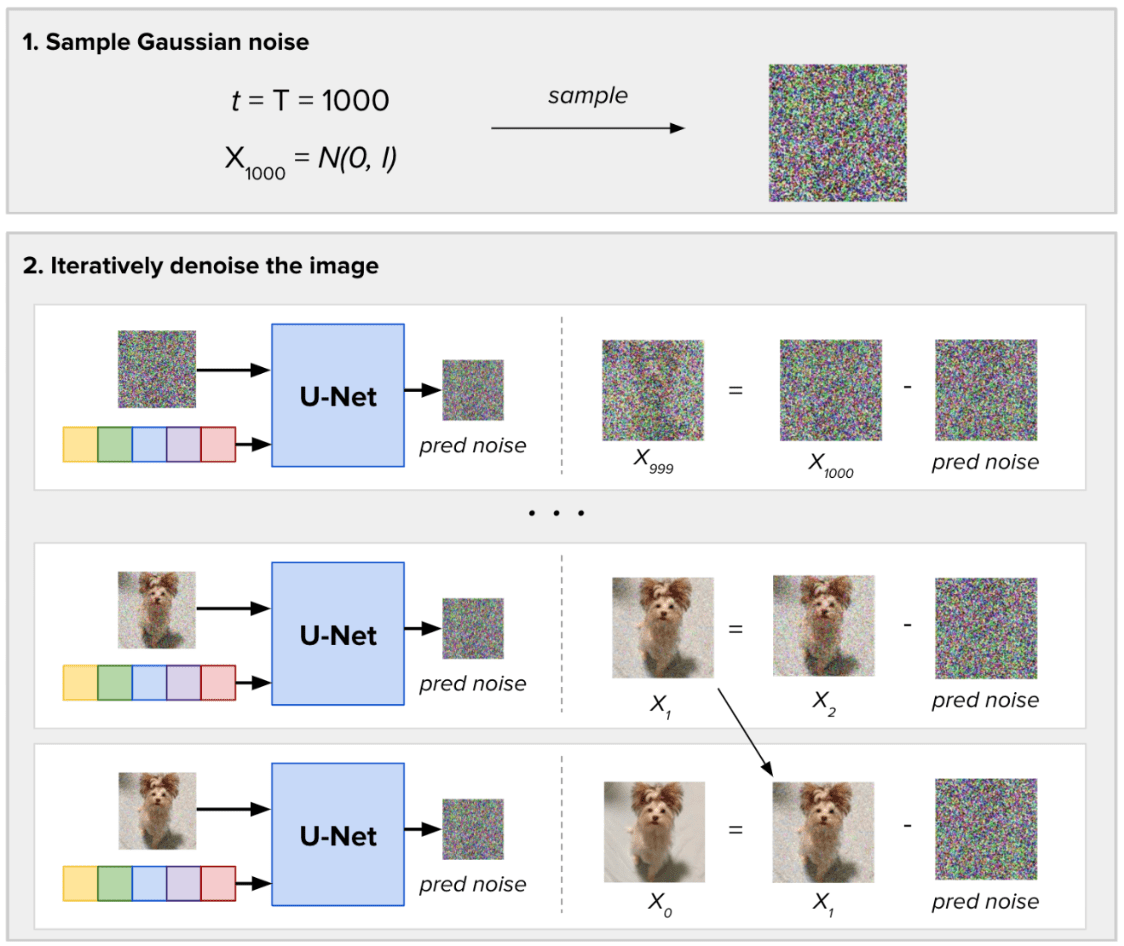
Proceso de eliminación de ruido para una sola imagen

Difusión estable

El proceso de difusión inversa en los modelos de difusión tradicionales implica pasar iterativamente una imagen de tamaño completo a través de la arquitectura U-Net para obtener el resultado final sin ruido. Sin embargo, esta naturaleza iterativa presenta desafíos en términos de eficiencia computacional. Esto se acentúa cuando se trata de imágenes de gran tamaño y un elevado número de etapas de difusión (T). El tiempo necesario para eliminar el ruido gaussiano de la imagen durante el muestreo puede llegar a ser prohibitivo. Para abordar este problema, un grupo de investigadores propuso un enfoque novedoso llamado Difusión estable, originalmente conocido como Modelo de difusión latente (LDM) [15]. Exploraremos los principales avances con respecto a los modelos de difusión presentados en este artículo: el trabajo con imágenes en el espacio latente y el condicionamiento.

Modelos de difusión latente

Stable Diffusion introduce una modificación clave al realizar el proceso de difusión en el espacio latente. Esto funciona mediante el uso de un entrenado Codificador E para codificar una imagen de tamaño completo en una representación de dimensión inferior (espacio latente). Luego, realiza el proceso de difusión directa y el proceso de difusión inversa dentro del espacio latente. Más tarde, con un entrenado Decodificador D, podemos decodificar la imagen desde su representación latente hasta el espacio de píxeles. Para construir el codificador y el decodificador, podemos entrenar alguna variante de Codificador automático variacional (VAE). Luego, esta red se desacopla para usar ambos componentes por separado.

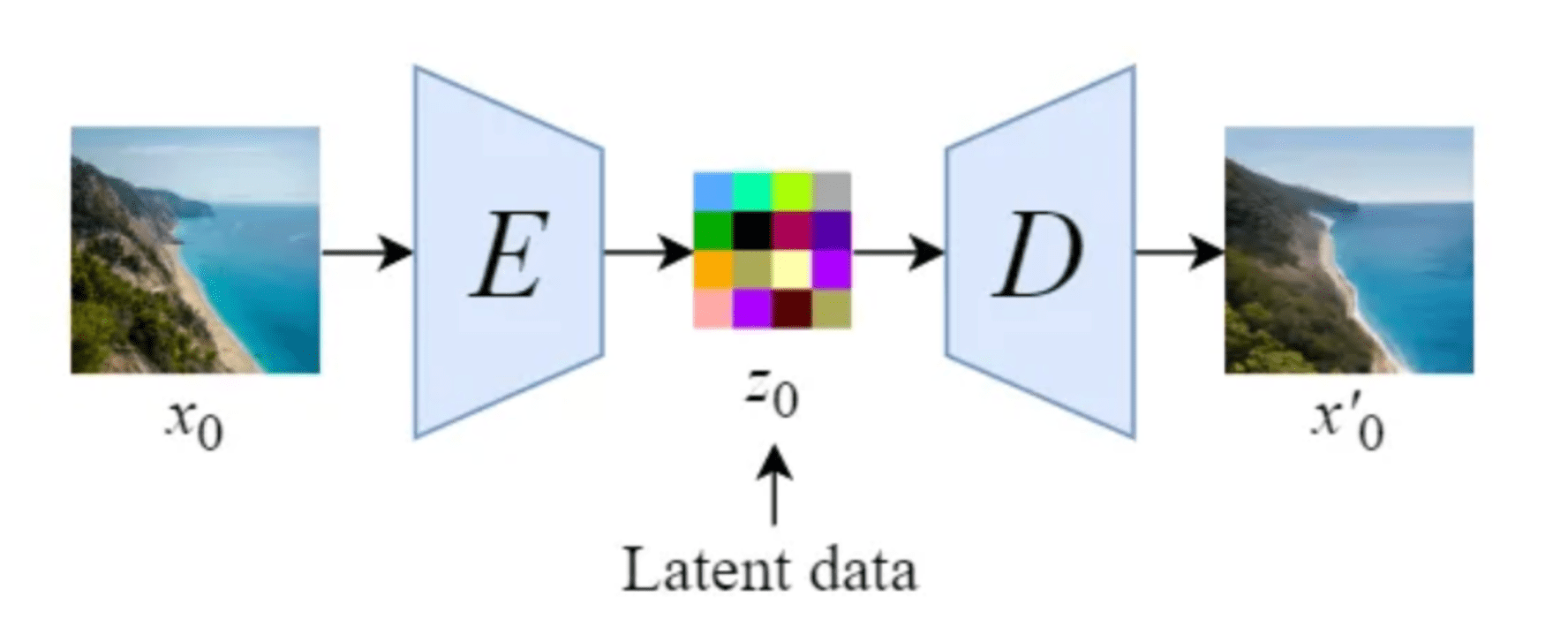
Ilustración de un codificador automático propuesto por el artículo Stable Diffusion [14]

Ilustración de una descripción general del modelo de difusión estable en el espacio latente [14]

El traslado de las operaciones de difusión al espacio latente en Stable Diffusion mejora la velocidad y reduce los costos. Este avance acelera los procesos de eliminación de ruido y muestreo, lo que lo convierte en una solución eficiente para la generación de imágenes de alta calidad y una formación estable. Al aprovechar el espacio latente, Stable Diffusion alivia la carga computacional en el proceso de difusión inversa. Esto permite eliminar el ruido de las imágenes más rápidamente, lo que mejora tanto la velocidad como la estabilidad y solidez generales del modelo.

Acondicionamiento

Hasta entonces, la generación de imágenes de una clase específica era posible principalmente mediante la adición de la etiqueta de clase en la entrada. Comúnmente conocido como Guía del clasificador. Sin embargo, una de las características más destacadas del modelo Stable Diffusion es su capacidad para generar imágenes basadas en indicaciones de texto específicas u otras entradas de condicionamiento. Esto se logra mediante la introducción de mecanismos de condicionamiento en el modelo de difusión interna, que también se considera en la literatura como Guía sin clasificadores (CFG) [16]. Para permitir el acondicionamiento, la U-Net de eliminación de ruido del modelo de difusión interna utiliza un mecanismo de atención cruzada. Esto permite que el modelo incorpore de manera efectiva la información de acondicionamiento durante el proceso de generación de imágenes (eliminación de ruido). Las entradas de acondicionamiento pueden adoptar diversas formas según la salida deseada:

• Las entradas de texto se transforman primero en incrustaciones a través de modelos lingüísticos como BERT o CLIP. En el condicionamiento, mapeamos estas incrustaciones en la U-Net utilizando una capa de atención con varios cabezales, representada como Q, K y V en el diagrama.
• Otras entradas de condicionamiento, como los datos alineados espacialmente, como los mapas semánticos, las imágenes o la pintura incrustada, actúan de manera similar. Sin embargo, la integración de estos mecanismos de condicionamiento generalmente se logra mediante la concatenación.

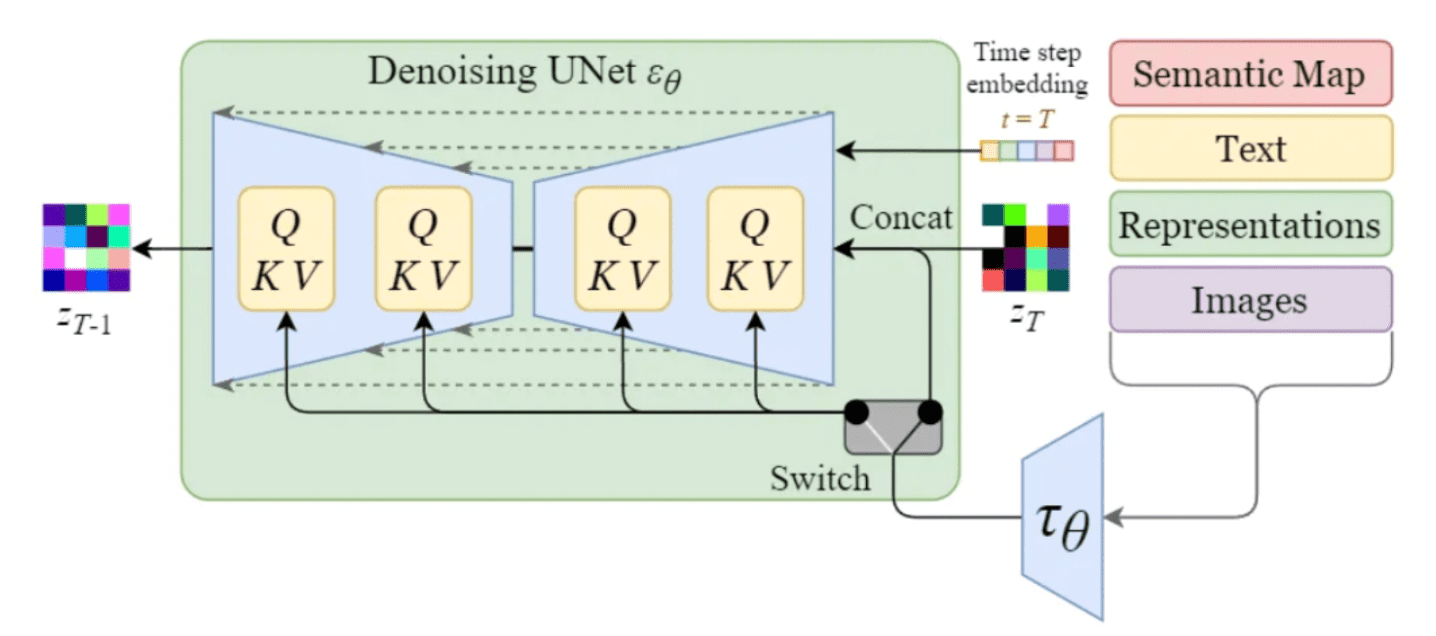
Mecanismo de acondicionamiento dentro de U-Net de Stable Diffusion [14]

Al incorporar mecanismos de acondicionamiento, el modelo Stable Diffusion amplía sus capacidades para generar imágenes basadas en entradas adicionales específicas. Las indicaciones de texto, los mapas semánticos o las imágenes adicionales permiten una síntesis de imágenes más versátil y controlada. Mediante el uso ingeniería rápida, es posible crear imágenes aún más atractivas. Si está interesado en conocer las mejores prácticas para aplicar la ingeniería rápida tanto a los modelos lingüísticos de gran tamaño como a los de difusión estable, consulte nuestra blog sobre ingeniería rápida.

Arquitectura

En nuestro recorrido por los modelos de difusión latente y el poder del acondicionamiento, podemos observar un avance notable en el mundo de la generación de imágenes. Ahora es el momento de ver cómo es todo el proceso de la difusión estable. Por un lado, durante formación, las imágenes (x₀) se codifican a través del Codificador E, alcanzando la representación latente de la imagen (z₀). En el proceso de difusión directa, la imagen se somete a la adición de ruido gaussiano, obteniendo una imagen ruidosa (z_T). Luego, la imagen pasó por la U-Net para predecir el ruido presente en z_T. Esta comparación entre el ruido real añadido en la difusión directa y la predicción permite calcular la pérdida mencionada anteriormente. Con la pérdida calculada, actualizamos los parámetros de la U-Net mediante la retropropagación.

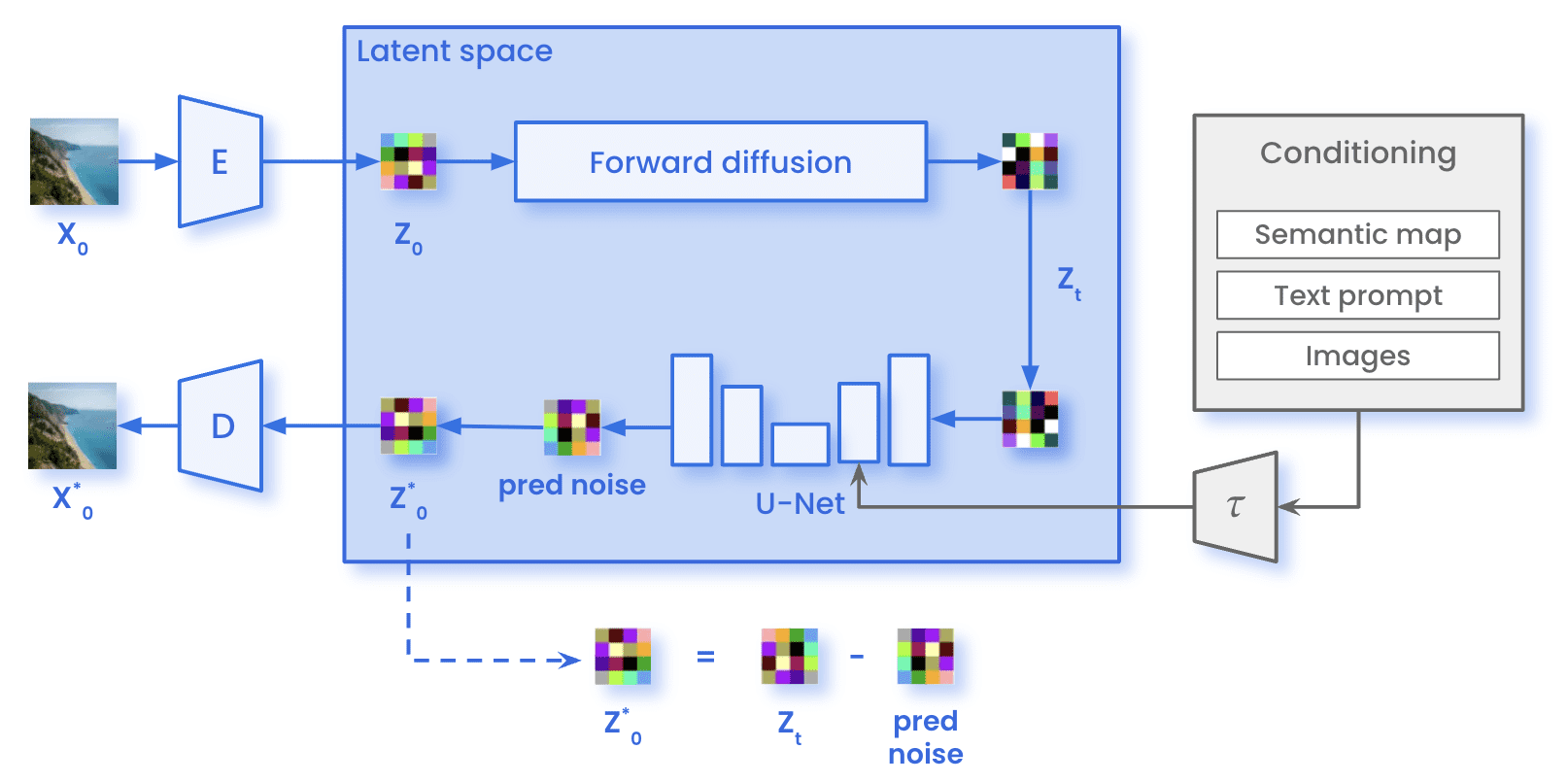
Arquitectura de difusión estable durante el entrenamiento

Por otro lado, el proceso de difusión directa no se produce durante el muestreo. Simplemente muestreamos el ruido gaussiano con las mismas dimensiones presentes en el espacio latente (z)_T). Este ruido pasa a través de la U-Net durante el número especificado de pasos de inferencia T. En cada paso t, la U-Net predice todo el ruido presente en la imagen. El modelo elimina solo una fracción del ruido previsto para obtener la representación de la imagen en el intervalo temporal t-1. Después de que todos los pasos de inferencia en T sean iterativos, obtenemos la representación dentro del espacio latente de la imagen generada (₀). Con el decodificador D, podemos transformar esa imagen del espacio latente al espacio de píxeles (X)₀).

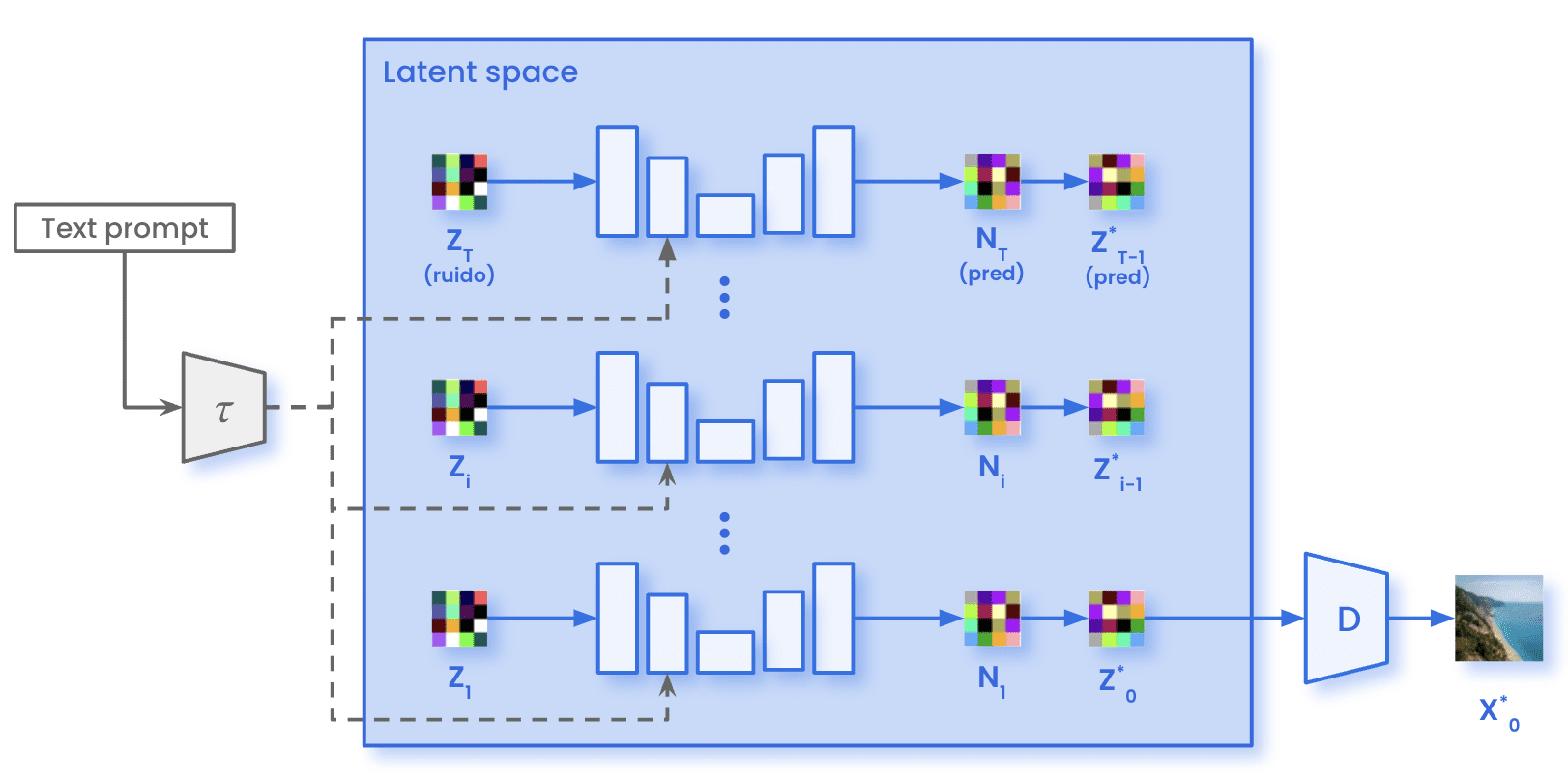
Arquitectura de difusión estable durante el muestreo

Casos de uso

Los modelos de difusión ofrecen soluciones versátiles para abordar diversos problemas. Algunos de los casos de uso más comunes en los que los modelos de difusión sobresalen son:

• Generación de imágenes mediante indicaciones: genere imágenes a partir de indicaciones textuales o entradas de acondicionamiento, lo que permite una síntesis de imágenes controlada y personalizable.
• Súper resolución de imagen: mejoran la resolución y la calidad de las imágenes de baja resolución, generando versiones de alta resolución con detalles y nitidez mejorados.
• Adaptación de dominio y transferencia de estilos: transferir el estilo o las características de una imagen o dominio a otro, lo que permite adaptar los modelos entrenados en un dominio de origen para que funcionen bien en un dominio de destino con diferentes características visuales.
• Imagen en pintura: rellena las partes faltantes o corruptas de una imagen, reconstruyendo los detalles faltantes para crear imágenes visualmente completas y coherentes.

• Pintura externa de imágenes: expandir la imagen más allá de sus fronteras creando continuidad y generando una imagen más grande.

La primera imagen es un ejemplo de lo que se puede hacer con Midjourney, tomada de la sección superior de su página web. La segunda imagen muestra un ejemplo de pintura para reemplazar al perro (mediante pintura) por un gato (mediante instrucciones) [15].

Conclusiones clave

En resumen, estas son las principales conclusiones que queremos que aprendas al leer este artículo:

• Los modelos de difusión constan de dos procesos: difusión directa y difusión inversa.
• El proceso de difusión directa consiste en añadir ruido gaussiano de forma iterativa. Al usar la fórmula de forma cerrada en un solo paso, eliminamos la necesidad de iterar. Esto permite una generación más rápida de las imágenes dañadas.
• El proceso de difusión inversa implica la utilización de una red neuronal para aproximarse al proceso de eliminación de ruido. Este proceso es iterativo, paso a paso, hasta recuperar la imagen original.
• Los modelos de difusión latente (LDM) mejoran la eficiencia de la generación de imágenes basadas en la difusión al realizar el proceso de difusión en el espacio latente. Este enfoque acelera significativamente el proceso de generación, especialmente en el caso de imágenes grandes y etapas de difusión más largas.
• Algunos modelos de difusión ofrecen la posibilidad de guiar la generación mediante el uso de entradas adicionales. Los textos y las imágenes son algunas de las entradas de guía más comunes.
• Los modelos de difusión han encontrado aplicaciones en varios casos de uso. Algunos de ellos son: la generación de imágenes mediante indicaciones, la pintura de imágenes, la adaptación de dominios o la transferencia de estilos y la superresolución de imágenes. Estos modelos ofrecen soluciones versátiles para tareas que van desde la síntesis creativa de imágenes hasta la mejora y restauración de imágenes.

En conclusión, los modelos de difusión se convirtieron en un nuevo paradigma efectivo para la generación y manipulación de imágenes. Al combinar los principios de los procesos de difusión con las técnicas de aprendizaje profundo, estos modelos ofrecen nuevas vías para generar imágenes de alta calidad. Esperamos que este blog sirva para comprender mejor cómo funcionan los modelos de difusión. ¡Y quédate atónito para ver más contenido relacionado en futuros blogs!

Referencias

• Redes generativas de confrontación Goodfellow y otros (2014)
• Modelos probabilísticos de difusión de ruido (DDPM), Ho y otros (2020)
• Los modelos de difusión superan a las GAN en la síntesis de imágenes, Dhariwal y Nichol (2021)
• Modelos probabilísticos de difusión de eliminación de ruido mejorados, Nichol y Dhariwal (2021)
• Síntesis de imágenes de alta resolución con modelos de difusión latente, Rombach y otros (2022)
• Guía de difusión sin clasificadores, Ho y Salimans (2022)
• Introducción a los modelos de difusión para el aprendizaje automático, Asamblea I (2022)
• La difusión estable ilustrada, Jay Alamar (2022)
• ¡El modelo de difusión se explica claramente!, Steins (2022)
• ¡La difusión estable se explica claramente!, Steins (2023)
• Una imagen generada por la IA ganó un premio de arte. Los artistas no están contentos, Kevin Roose (2022)
• Cómo funcionan los modelos de difusión: las matemáticas desde cero, Karagiannakos y Adaloglouon (2022)
• ¿Qué son los modelos de difusión?, Lilian Weng (2022)