Introdução

Já ouviu falar do cachorro de Pavlov? Em 1897, Ivan Pavlov, fisiologista russo, publicou suas descobertas sobre comportamento condicionado, demonstrando como os cães podem ser condicionados a associar um estímulo não condicionado (comida) a um estímulo neutro (sino), levando a uma resposta condicionada (salivação) desencadeada apenas pelo sino.

A ideia por trás desse experimento é que o cão possa ser condicionado a se comportar de uma determinada maneira de acordo com uma série de recompensas ou punições que recebeu, que é a ideia central por trás do aprendizado por reforço. Tanto o cão de Pavlov quanto os sistemas de aprendizado por reforço mostram o poder do condicionamento e a capacidade de adaptar comportamentos com base em sinais de reforço.

Neste blog, vamos explorar os fundamentos do aprendizado por reforço, aprendendo de cima para baixo. Este blog é destinado a leitores com algum conhecimento de cálculo e álgebra, mas você não precisa ser um especialista para continuar.

O que é aprendizado por reforço?

O aprendizado por reforço é uma abordagem matemática para aprender por tentativa e erro e busca emular uma das maneiras pelas quais os animais aprendem. Imagine que você tenha um cachorrinho pequeno a quem deseja ensinar truques. Eles aprenderão a fazer esses truques por tentativa e erro, caindo, ocasionalmente esbarrando na mobília (feedback negativo), mas também sendo elogiados por você e recompensados quando conseguirem progredir (feedback positivo). Ao longo de muitas tentativas, eles aprenderão progressivamente como realizar melhor os truques e, eventualmente, sozinhos, sem a necessidade de guloseimas. Esse é o fenômeno com o qual o aprendizado por reforço tenta aprender.

A ideia principal por trás do aprendizado por reforço é que um agente (um modelo, mas em nosso exemplo anterior, o filhote) aprenderá com o ambiente (neste caso, você e seu entorno) interagindo com ele (tentando o truque, caindo) e recebendo feedback (sendo elogiado, recebendo guloseimas) cada vez que interagir de uma maneira diferente. Cada interação é conhecida como ação (o movimento que o cão faz) e o feedback recebido é dado por um recompensa função (o tratamento que lhe damos ou negamos), que pode ser positiva ou negativa caso uma ação tenha uma consequência negativa.

[caption id="attachment_2328" align="aligncenter” width="665"]

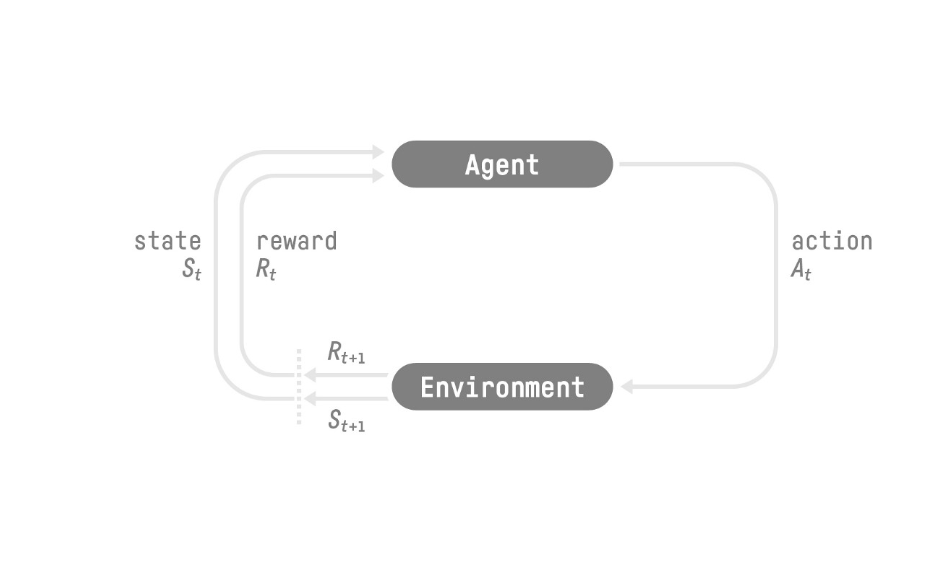
Imagem retirada de Reinforcement Learning An Introduction [/caption]

Na figura acima, St, At, Rt, referem-se ao estado, ação e recompensa no tempo t. No exemplo do filhote, o estado se referiria a qualquer posição em que o cão estivesse no momento t, à ação, ao movimento que ele está realizando e à recompensa se você vai ou não alimentá-lo com uma guloseima.

Ação e espaço estatal

Os cenários de aprendizado por reforço têm um estado ou espaço de observação associado, ou seja, uma descrição completa ou parcial do ambiente. Por exemplo, no caso de um agente aprendendo a jogar xadrez, o agente tem uma descrição completa do ambiente, pois conhece a posição de todas as outras peças no tabuleiro em uma determinada etapa. Descrições completas do ambiente prontamente disponíveis não são a regra e descrições parciais são conhecidas como observações.

Esses tipos de cenários também têm um espaço de ação associado, ou seja, o conjunto de todas as ações possíveis que um agente pode realizar. Esse espaço de ação pode ser discreto, como no caso do jogo de xadrez, onde há um conjunto de ações possíveis que uma determinada peça pode realizar, ou contínuo, como o espaço de ação ao dirigir um carro.

Modelo de recompensa O modelo de recompensa é o núcleo do aprendizado por reforço, pois fornece ao agente o feedback de que ele precisa para aprender. A recompensa de uma trajetória (no xadrez, por exemplo, uma trajetória pode significar simplesmente uma série de ações sequenciais que o agente realiza) é dada pela soma das recompensas descontadas em cada etapa de tempo:

R (τ) =r (t+1) +r (t+2) +... +k-1r (t+k)

R é a função de recompensa cumulativa ao longo de toda a trajetória τ e é composta pela recompensa obtida em cada etapa de tempo de 1 a k necessária para completar τ.

é conhecida como taxa de desconto e sua introdução é necessária, pois recompensas mais distantes do estado atual têm menos probabilidade de acontecer do que aquelas mais próximas do estado atual. Pense desta forma: se você está jogando xadrez e planejando uma série de 4 movimentos para pegar a rainha do seu adversário, ele poderia mover sua rainha antes de você alcançá-la ou pegar uma de suas peças, o que era fundamental para sua estratégia e, portanto, você não conseguiria completar sua jogada. Recompensas mais distantes do estado atual precisam ser descontadas, pois têm menos probabilidade de acontecer do que aquelas mais próximas ao estado.

Tipos de aprendizado por reforço:

Mas como esses agentes aprendem com o meio ambiente? Como eles sabem qual ação tomar em qualquer estado para maximizar sua recompensa cumulativa? Bem, é aqui que a política entra em jogo. A política de uma tarefa de aprendizado por reforço, notada π, é o modelo que diz ao agente como se comportar em qualquer estado. Essa é a função que pretendemos aprender para encontrar a política ótima π que maximize a recompensa cumulativa do agente.

Existem duas abordagens principais para encontrar π: métodos baseados em políticas e métodos baseados em valores. Por um lado, os métodos baseados em valores visam aprender uma função de valor que mapeia o estado para o valor esperado de estar nesse estado. A política usada nesse cenário é simplesmente realizar a ação que leva ao estado com o maior valor.

Por outro lado, os métodos baseados em políticas visam aprender diretamente a função π, ou seja, um mapeamento de qual ação é melhor tomar em cada estado. Essa política pode ser determinística (para um determinado estado S, a ação ideal é sempre A) ou estocástica, produzindo uma distribuição de probabilidade sobre todas as ações em cada estado.

[caption id="attachment_2344" align="aligncenter” width="817"]

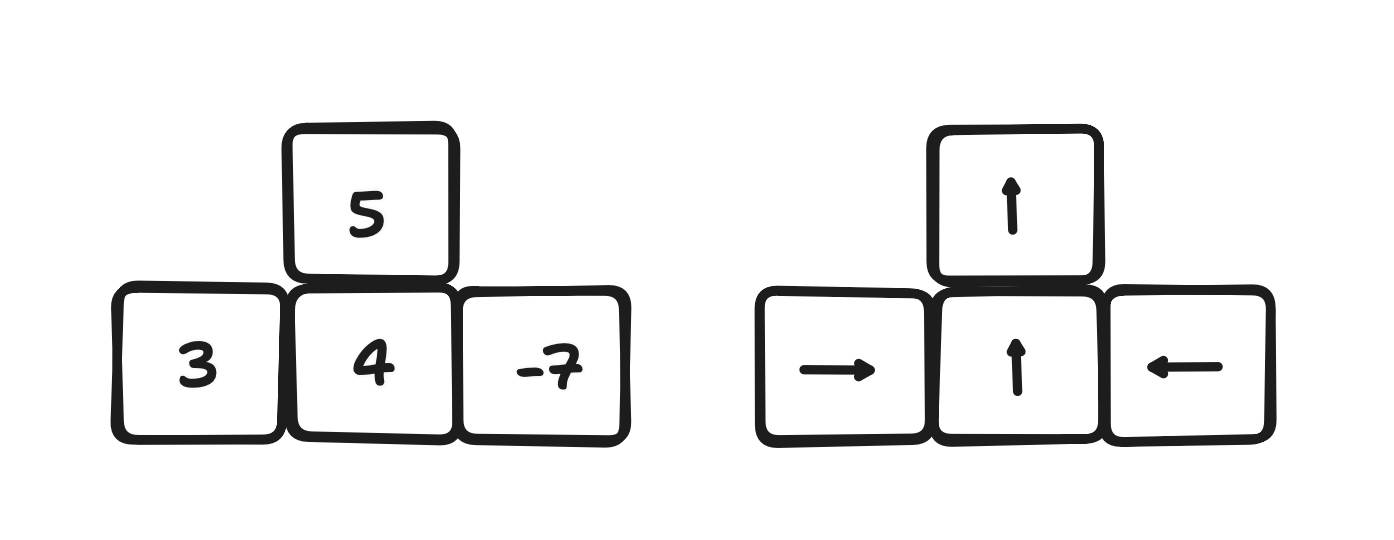
Métodos baseados em valor versus métodos baseados em políticas [/caption]

Gradientes de política

Uma das principais abordagens para o aprendizado de políticas estocásticas é o uso de uma rede neural cujos parâmetros são ajustados usando gradiente descendente, um processo chamado gradientes de política. A abordagem mais simples adotada é o gradiente de política, que simplesmente atualiza os parâmetros da política por meio de uma regra de aprendizado muito parecida com a usada no aprendizado supervisionado:

← + J ()

Onde é o vetor com todos os parâmetros que compõem a política, é uma taxa de aprendizado predefinida e J () é o gradiente da função de custo J (a função que mede a distância entre a política e a resposta ideal) em relação aos parâmetros. Essa estrutura se assemelha à descida mais íngreme de uma rede neural em um problema de aprendizado supervisionado, e a regra de atualização também é muito semelhante, visto que, em geral, as políticas são aproximadas usando redes neurais.

Mas o gradiente político sofre de grandes desvantagens:

• É uma abordagem de aprendizado de Monte Carlo (que significa calcular a média da recompensa que o agente recebe em um episódio inteiro), levando em consideração a trajetória total da recompensa (uma amostra), que geralmente sofre de alta variação, o que leva a problemas de convergência.
• As amostras são usadas apenas uma vez, uma vez que a política é atualizada, a nova política é usada para amostrar uma nova trajetória, o que é um processo caro
• Escolher a taxa de aprendizado correta () é difícil e o sistema sofre com gradientes que desaparecem e explodem, o que faz com que a convergência seja muito dependente da amostra.

Otimização da política proximal

Para lidar com essas e outras desvantagens dos gradientes de política, vários outros algoritmos foram explorados. Os modelos atuais de última geração são aqueles derivados da Proximal Policy Optimization (PPO), uma artigo publicado em 2017. A matemática por trás disso é desafiadora e excede o escopo desta revisão, mas, essencialmente, o PPO melhora o gradiente de políticas de duas maneiras principais:

• O PPO introduz um termo de divergência de metas, que penaliza os casos em que a política atualizada produz resultados muito diferentes das amostras anteriores. Gostaríamos que nossa política retornasse resultados dentro de um determinado bairro, para que as respostas sejam semelhantes de uma etapa para a seguinte.
• Como essa divergência limita a diferença entre duas amostras consecutivas, isso significa que as atualizações da política são pequenas e, portanto, as amostras podem ser reutilizadas mais de uma vez para atualizar a política.

Aprendizagem por reforço a partir do feedback humano

Em um nível abstrato, examinamos algumas das abordagens usadas no aprendizado por reforço. Mas como exatamente você treina um agente para resolver um problema real, já que não sabemos o valor da recompensa para nenhum estado no espaço estadual? Bem, a abordagem mais usada atualmente é o aprendizado por reforço a partir do feedback humano (RLHF).

[caption id="attachment_2329" align="aligncenter” width="833"]

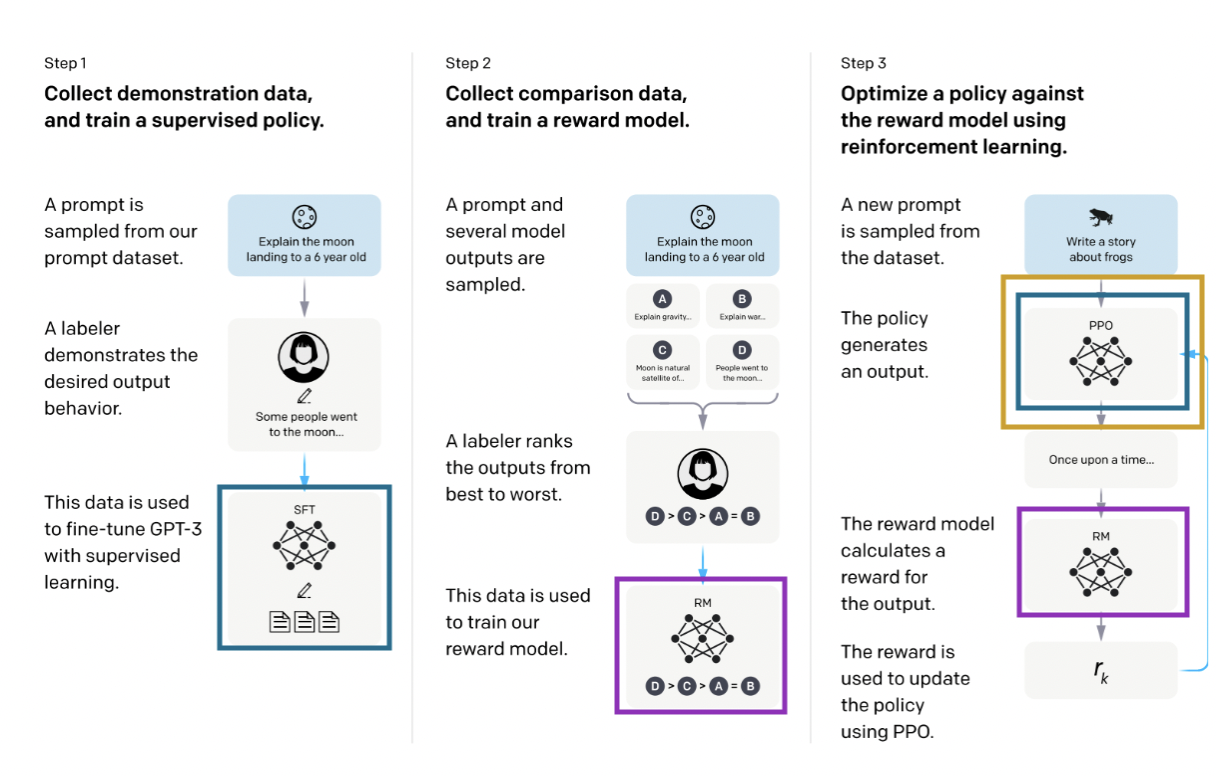
Imagem retirada de modelos de linguagem de treinamento para seguir as instruções com feedback humano [/caption]

O processo tem três etapas. A etapa 1 é treinar uma política supervisionada (em azul no diagrama acima), o que significa simplesmente treinar uma rede neural. Aqui, política e rede neural são sinônimos. Então, na etapa 2, vários resultados da política são classificados do melhor para o pior pelos rotuladores (outras abordagens incluem atribuir uma pontuação a cada saída) e essa entrada é usada na etapa 3 para treinar o que chamamos de modelo de recompensa (em roxo), outra rede neural que extrairá um resultado de uma política e lhe concederá uma recompensa. Esse modelo de recompensa é então usado para atualizar a política usando o PPO (em amarelo), onde, para cada etapa de treinamento, a saída do PPO é pontuada pelo modelo de recompensa.

Essa modalidade de treinamento de primeiro treinamento, uma política supervisionada que é então ajustada usando o aprendizado por reforço, tem sido amplamente utilizada recentemente, sendo seu exemplo mais famoso o ChatGPT. Outras áreas em que o PPO é amplamente utilizado são a negociação de ações e a robótica.

Estudo de caso: Escrevendo resenhas positivas de filmes

Um dos repositórios mais completos para ajustar modelos usando o aprendizado por reforço é TRL, que pode ser usado para ajustar os transformadores. Nós o testamos ajustando o GPT-2 para produzir críticas positivas de filmes, usando o conjunto de dados do IMDB. Usamos um modelo pré-treinado do DistilBert para realizar a análise de sentimentos sobre as avaliações e o usamos como nosso modelo de recompensa.

Duas cópias do GPT-2 foram usadas: uma congelada, sendo treinada apenas usando aprendizado supervisionado, e outra cujos pesos foram alterados a cada iteração para comparar o comportamento passado e o atual.

[caption id="attachment_2331" align="aligncenter” width="907"]

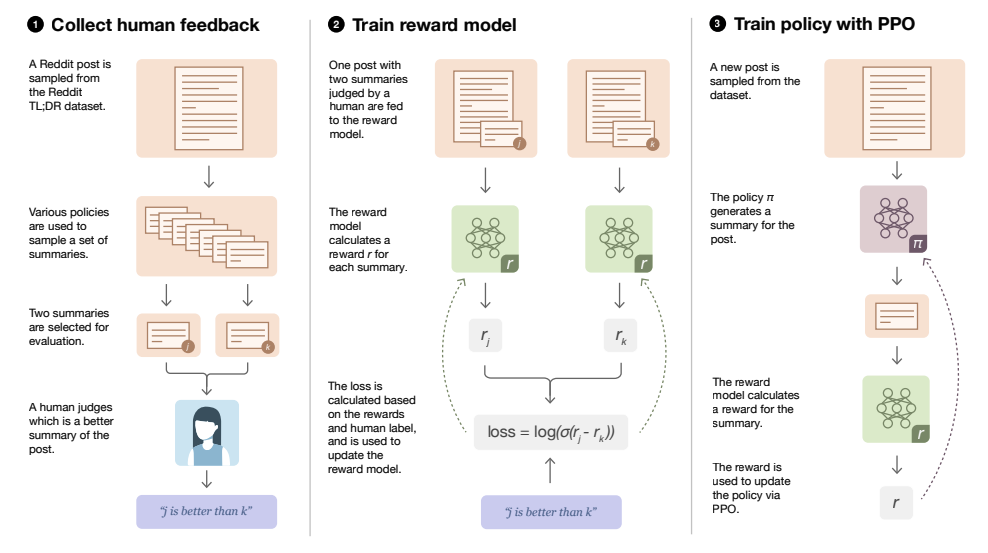
Imagem retirada da Implementação do RLHF: Aprendendo a resumir com o TrlX [/caption]

No diagrama, Prompt simplesmente se refere a uma descrição incompleta que o GPT precisa concluir. Ao realizar a análise de sentimentos sobre as duas saídas, a recompensa da saída atual do modelo ajustado é calculada e, com isso, seus pesos são modificados. Um exemplo do desempenho do modelo antes e depois do ajuste fino é mostrado abaixo.

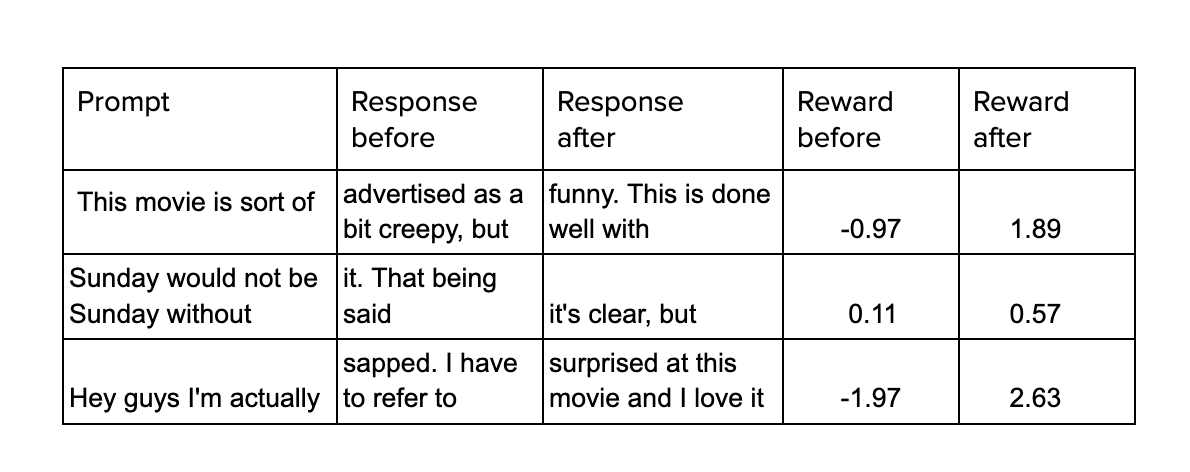
Conclusões

Neste artigo, examinamos os fundamentos do aprendizado por reforço, partindo de conceitos-chave, como espaço de estados, espaço de ação e modelo de recompensa, até como usar o feedback humano para ajustar os modelos de linguagem. Mencionamos algumas áreas nas quais o aprendizado por reforço é particularmente usado e usamos um aplicativo, escrevendo críticas positivas para filmes. Atualmente, o aprendizado por reforço com técnicas de feedback humano está na moda na fase de ajuste fino de grandes modelos de linguagem, mas pode ser usado em uma ampla série de cenários em que uma função de recompensa pode ser construída para orientar o processo de aprendizagem.

Referências

Sutton, R., Barton, A. 'Aprendizagem por reforço: uma introdução', 2018

Schulman, J., et al, 'Algoritmos de otimização de políticas proximais', 2017

Ouyang, L., et al, 'Treinar modelos de linguagem para seguir instruções com feedback humano', 2022